Question-134255

Question Number 134255 by shaker last updated on 01/Mar/21

Commented by Dwaipayan Shikari last updated on 01/Mar/21

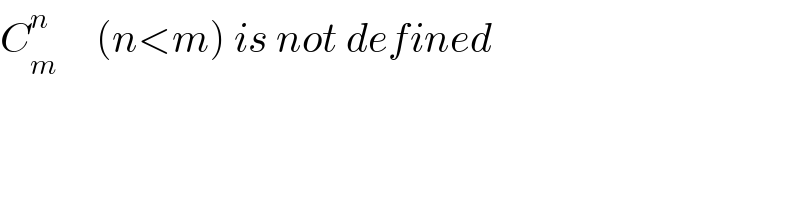
$${C}_{{m}} ^{{n}} \:\:\:\:\:\left({n}<{m}\right)\:{is}\:{not}\:{defined} \\ $$

Commented by mr W last updated on 01/Mar/21

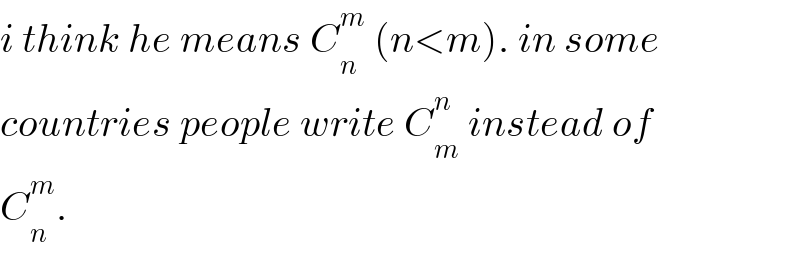
i think he means C_n ^m (n<m). in some countries people write C_m ^n instead of C_n ^m .

$${i}\:{think}\:{he}\:{means}\:{C}_{{n}} ^{{m}} \:\left({n}<{m}\right).\:{in}\:{some}\: \\ $$$${countries}\:{people}\:{write}\:{C}_{{m}} ^{{n}} \:{instead}\:{of} \\ $$$${C}_{{n}} ^{{m}} . \\ $$

Answered by EDWIN88 last updated on 01/Mar/21

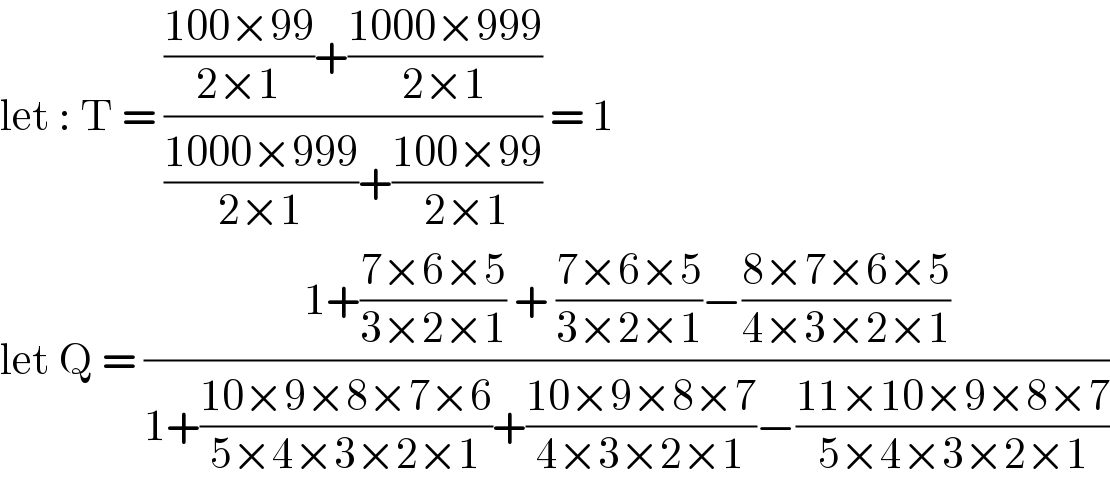
let : T = ((((100×99)/(2×1))+((1000×999)/(2×1)))/(((1000×999)/(2×1))+((100×99)/(2×1)))) = 1 let Q = ((1+((7×6×5)/(3×2×1)) + ((7×6×5)/(3×2×1))−((8×7×6×5)/(4×3×2×1)))/(1+((10×9×8×7×6)/(5×4×3×2×1))+((10×9×8×7)/(4×3×2×1))−((11×10×9×8×7)/(5×4×3×2×1))))

$$\mathrm{let}\::\:\mathrm{T}\:=\:\frac{\frac{\mathrm{100}×\mathrm{99}}{\mathrm{2}×\mathrm{1}}+\frac{\mathrm{1000}×\mathrm{999}}{\mathrm{2}×\mathrm{1}}}{\frac{\mathrm{1000}×\mathrm{999}}{\mathrm{2}×\mathrm{1}}+\frac{\mathrm{100}×\mathrm{99}}{\mathrm{2}×\mathrm{1}}}\:=\:\mathrm{1} \\ $$$$\mathrm{let}\:\mathrm{Q}\:=\:\frac{\mathrm{1}+\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}}{\mathrm{3}×\mathrm{2}×\mathrm{1}}\:+\:\frac{\mathrm{7}×\mathrm{6}×\mathrm{5}}{\mathrm{3}×\mathrm{2}×\mathrm{1}}−\frac{\mathrm{8}×\mathrm{7}×\mathrm{6}×\mathrm{5}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}}{\mathrm{1}+\frac{\mathrm{10}×\mathrm{9}×\mathrm{8}×\mathrm{7}×\mathrm{6}}{\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}+\frac{\mathrm{10}×\mathrm{9}×\mathrm{8}×\mathrm{7}}{\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}−\frac{\mathrm{11}×\mathrm{10}×\mathrm{9}×\mathrm{8}×\mathrm{7}}{\mathrm{5}×\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1}}} \\ $$

Answered by Ñï= last updated on 01/Mar/21

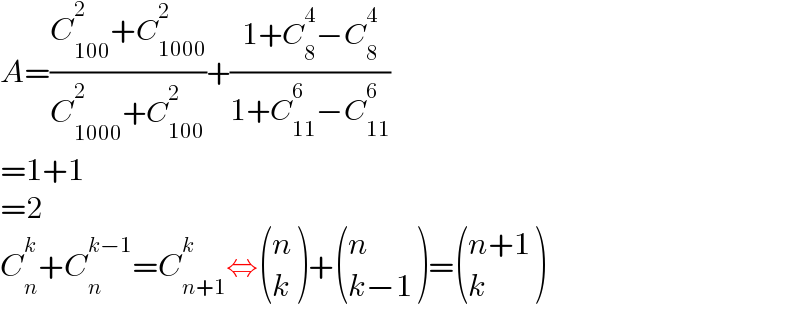
A=((C_(100) ^2 +C_(1000) ^2 )/(C_(1000) ^2 +C_(100) ^2 ))+((1+C_8 ^4 −C_8 ^4 )/(1+C_(11) ^6 −C_(11) ^6 )) =1+1 =2 C_n ^k +C_n ^(k−1) =C_(n+1) ^k ⇔ ((n),(k) )+ ((n),((k−1)) )= (((n+1)),(k) )

$${A}=\frac{{C}_{\mathrm{100}} ^{\mathrm{2}} +{C}_{\mathrm{1000}} ^{\mathrm{2}} }{{C}_{\mathrm{1000}} ^{\mathrm{2}} +{C}_{\mathrm{100}} ^{\mathrm{2}} }+\frac{\mathrm{1}+{C}_{\mathrm{8}} ^{\mathrm{4}} −{C}_{\mathrm{8}} ^{\mathrm{4}} }{\mathrm{1}+{C}_{\mathrm{11}} ^{\mathrm{6}} −{C}_{\mathrm{11}} ^{\mathrm{6}} } \\ $$$$=\mathrm{1}+\mathrm{1} \\ $$$$=\mathrm{2} \\ $$$${C}_{{n}} ^{{k}} +{C}_{{n}} ^{{k}−\mathrm{1}} ={C}_{{n}+\mathrm{1}} ^{{k}} \Leftrightarrow\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}+\begin{pmatrix}{{n}}\\{{k}−\mathrm{1}}\end{pmatrix}=\begin{pmatrix}{{n}+\mathrm{1}}\\{{k}}\end{pmatrix} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply