Menu Close

Question-134327

Tinku Tara 0 Comments
Pin




Question Number 134327 by mr W last updated on 02/Mar/21
Answered by aleks041103 last updated on 25/Dec/21
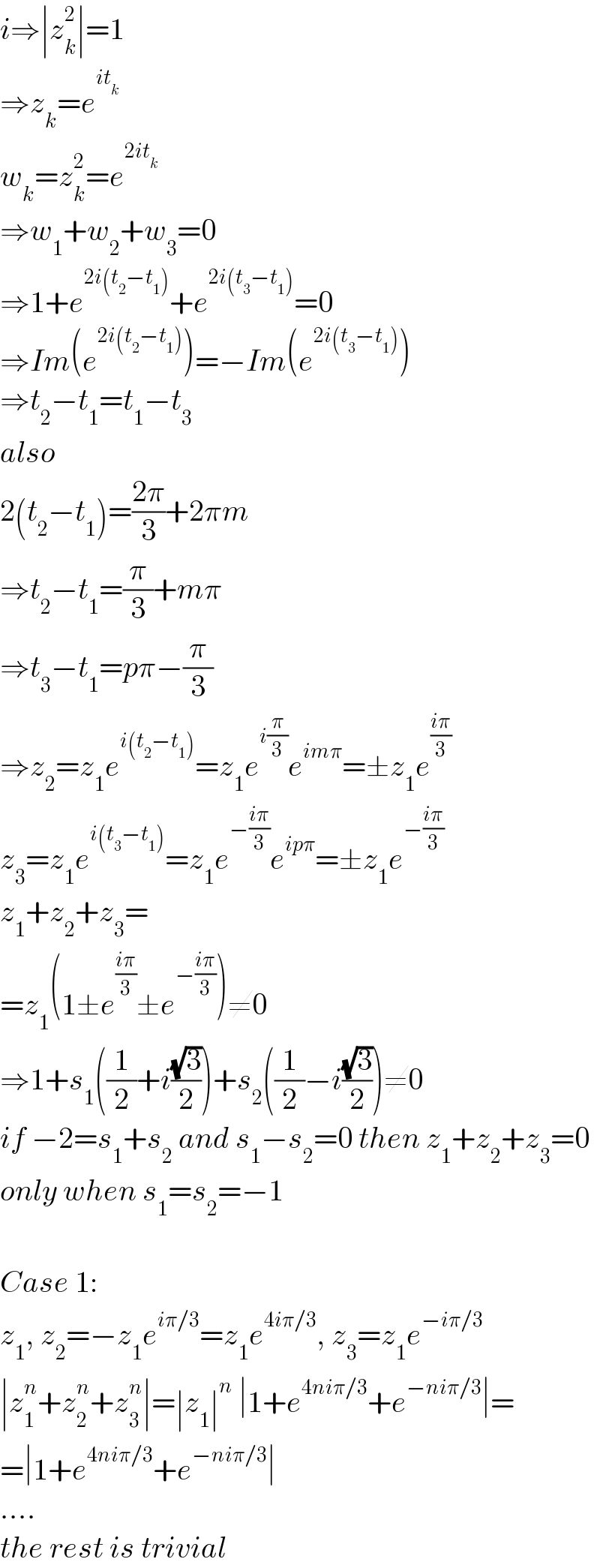
i⇒∣z_k ^2 ∣=1 ⇒z_k =e^(it_k ) w_k =z_k ^2 =e^(2it_k ) ⇒w_1 +w_2 +w_3 =0 ⇒1+e^(2i(t_2 −t_1 )) +e^(2i(t_3 −t_1 )) =0 ⇒Im(e^(2i(t_2 −t_1 )) )=−Im(e^(2i(t_3 −t_1 )) ) ⇒t_2 −t_1 =t_1 −t_3 also 2(t_2 −t_1 )=((2π)/3)+2πm ⇒t_2 −t_1 =(π/3)+mπ ⇒t_3 −t_1 =pπ−(π/3) ⇒z_2 =z_1 e^(i(t_2 −t_1 )) =z_1 e^(i(π/3)) e^(imπ) =±z_1 e^((iπ)/3) z_3 =z_1 e^(i(t_3 −t_1 )) =z_1 e^(−((iπ)/3)) e^(ipπ) =±z_1 e^(−((iπ)/3)) z_1 +z_2 +z_3 = =z_1 (1±e^((iπ)/3) ±e^(−((iπ)/3)) )≠0 ⇒1+s_1 ((1/2)+i((√3)/2))+s_2 ((1/2)−i((√3)/2))≠0 if −2=s_1 +s_2 and s_1 −s_2 =0 then z_1 +z_2 +z_3 =0 only when s_1 =s_2 =−1 Case 1: z_1 , z_2 =−z_1 e^(iπ/3) =z_1 e^(4iπ/3) , z_3 =z_1 e^(−iπ/3) ∣z_1 ^n +z_2 ^n +z_3 ^n ∣=∣z_1 ∣^n ∣1+e^(4niπ/3) +e^(−niπ/3) ∣= =∣1+e^(4niπ/3) +e^(−niπ/3) ∣ .... the rest is trivial
$${i}\Rightarrow\mid{z}_{{k}} ^{\mathrm{2}} \mid=\mathrm{1} \\ $$$$\Rightarrow{z}_{{k}} ={e}^{{it}_{{k}} } \\ $$$${w}_{{k}} ={z}_{{k}} ^{\mathrm{2}} ={e}^{\mathrm{2}{it}_{{k}} } \\ $$$$\Rightarrow{w}_{\mathrm{1}} +{w}_{\mathrm{2}} +{w}_{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}+{e}^{\mathrm{2}{i}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)} +{e}^{\mathrm{2}{i}\left({t}_{\mathrm{3}} −{t}_{\mathrm{1}} \right)} =\mathrm{0} \\ $$$$\Rightarrow{Im}\left({e}^{\mathrm{2}{i}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)} \right)=−{Im}\left({e}^{\mathrm{2}{i}\left({t}_{\mathrm{3}} −{t}_{\mathrm{1}} \right)} \right) \\ $$$$\Rightarrow{t}_{\mathrm{2}} −{t}_{\mathrm{1}} ={t}_{\mathrm{1}} −{t}_{\mathrm{3}} \\ $$$${also} \\ $$$$\mathrm{2}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)=\frac{\mathrm{2}\pi}{\mathrm{3}}+\mathrm{2}\pi{m} \\ $$$$\Rightarrow{t}_{\mathrm{2}} −{t}_{\mathrm{1}} =\frac{\pi}{\mathrm{3}}+{m}\pi \\ $$$$\Rightarrow{t}_{\mathrm{3}} −{t}_{\mathrm{1}} ={p}\pi−\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow{z}_{\mathrm{2}} ={z}_{\mathrm{1}} {e}^{{i}\left({t}_{\mathrm{2}} −{t}_{\mathrm{1}} \right)} ={z}_{\mathrm{1}} {e}^{{i}\frac{\pi}{\mathrm{3}}} {e}^{{im}\pi} =\pm{z}_{\mathrm{1}} {e}^{\frac{{i}\pi}{\mathrm{3}}} \\ $$$${z}_{\mathrm{3}} ={z}_{\mathrm{1}} {e}^{{i}\left({t}_{\mathrm{3}} −{t}_{\mathrm{1}} \right)} ={z}_{\mathrm{1}} {e}^{−\frac{{i}\pi}{\mathrm{3}}} {e}^{{ip}\pi} =\pm{z}_{\mathrm{1}} {e}^{−\frac{{i}\pi}{\mathrm{3}}} \\ $$$${z}_{\mathrm{1}} +{z}_{\mathrm{2}} +{z}_{\mathrm{3}} = \\ $$$$={z}_{\mathrm{1}} \left(\mathrm{1}\pm{e}^{\frac{{i}\pi}{\mathrm{3}}} \pm{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\neq\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}+{s}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)+{s}_{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}−{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\neq\mathrm{0} \\ $$$${if}\:−\mathrm{2}={s}_{\mathrm{1}} +{s}_{\mathrm{2}} \:{and}\:{s}_{\mathrm{1}} −{s}_{\mathrm{2}} =\mathrm{0}\:{then}\:{z}_{\mathrm{1}} +{z}_{\mathrm{2}} +{z}_{\mathrm{3}} =\mathrm{0} \\ $$$${only}\:{when}\:{s}_{\mathrm{1}} ={s}_{\mathrm{2}} =−\mathrm{1} \\ $$$$ \\ $$$${Case}\:\mathrm{1}: \\ $$$${z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} =−{z}_{\mathrm{1}} {e}^{{i}\pi/\mathrm{3}} ={z}_{\mathrm{1}} {e}^{\mathrm{4}{i}\pi/\mathrm{3}} ,\:{z}_{\mathrm{3}} ={z}_{\mathrm{1}} {e}^{−{i}\pi/\mathrm{3}} \\ $$$$\mid{z}_{\mathrm{1}} ^{{n}} +{z}_{\mathrm{2}} ^{{n}} +{z}_{\mathrm{3}} ^{{n}} \mid=\mid{z}_{\mathrm{1}} \mid^{{n}} \:\mid\mathrm{1}+{e}^{\mathrm{4}{ni}\pi/\mathrm{3}} +{e}^{−{ni}\pi/\mathrm{3}} \mid= \\ $$$$=\mid\mathrm{1}+{e}^{\mathrm{4}{ni}\pi/\mathrm{3}} +{e}^{−{ni}\pi/\mathrm{3}} \mid \\ $$$$…. \\ $$$${the}\:{rest}\:{is}\:{trivial} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *