Question Number 134341 by Eric002 last updated on 02/Mar/21
Answered by mr W last updated on 02/Mar/21

Commented by mr W last updated on 02/Mar/21

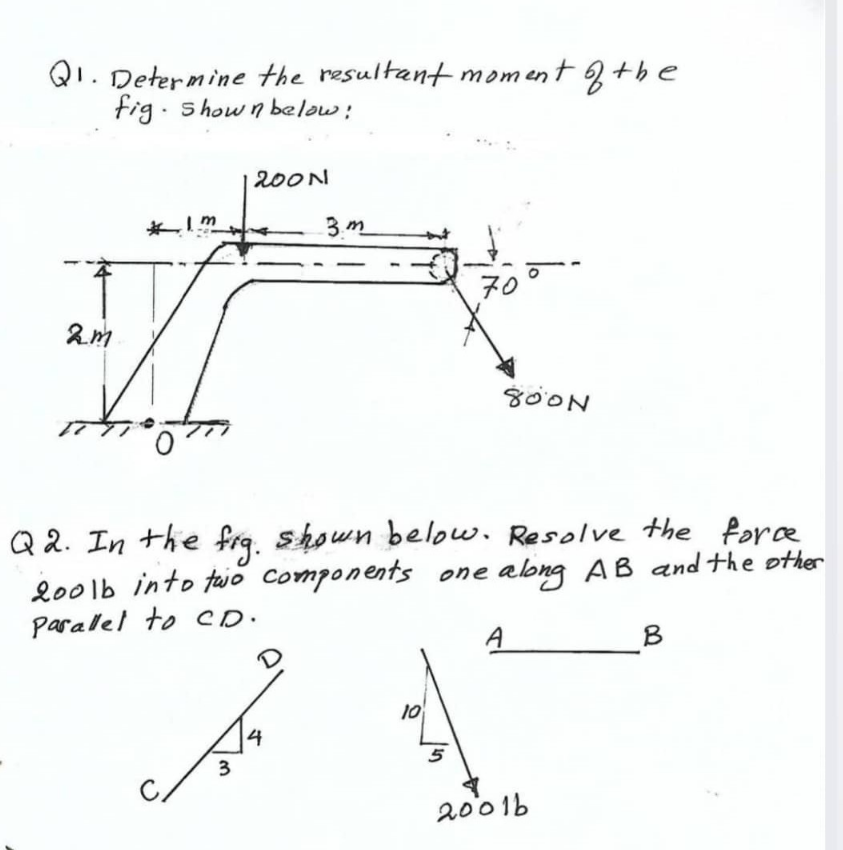
$${Q}\mathrm{1} \\ $$$${M}=\mathrm{200}×\mathrm{1}+\mathrm{800}×\mathrm{sin}\:\mathrm{70}°×\left(\mathrm{3}+\mathrm{1}\right)+\mathrm{800}×\mathrm{cos}\:\mathrm{70}°×\mathrm{2} \\ $$$$\approx\mathrm{2798}\:{Nm} \\ $$$$ \\ $$$${Q}\mathrm{2} \\ $$$$\mathrm{tan}\:\alpha=\frac{\mathrm{10}}{\mathrm{5}}=\mathrm{2}\:\Rightarrow\mathrm{sin}\:\alpha=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}},\:\mathrm{cos}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{4}}{\mathrm{3}}\:\Rightarrow\mathrm{sin}\:\beta=\frac{\mathrm{4}}{\mathrm{5}} \\ $$$${F}=\mathrm{200}\:{lb} \\ $$$${F}_{\mathrm{1}} ={component}\:{along}\:{AB} \\ $$$${F}_{\mathrm{2}} ={component}\:{parallel}\:{to}\:{CD} \\ $$$$\frac{{F}_{\mathrm{1}} }{\mathrm{sin}\:\left(\alpha+\beta\right)}=\frac{{F}_{\mathrm{2}} }{\mathrm{sin}\:\alpha}=\frac{{F}}{\mathrm{sin}\:\beta} \\ $$$${F}_{\mathrm{1}} =\frac{\mathrm{sin}\:\left(\alpha+\beta\right)}{\mathrm{sin}\:\beta}×{F}=\left(\frac{\mathrm{sin}\:\alpha}{\mathrm{tan}\:\beta}+\mathrm{cos}\:\alpha\right)×{F} \\ $$$$=\left(\frac{\mathrm{2}×\mathrm{3}}{\:\sqrt{\mathrm{5}}×\mathrm{4}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)×\mathrm{200}=\mathrm{100}\sqrt{\mathrm{5}}=\mathrm{223}.\mathrm{6}\:{lb} \\ $$$${F}_{\mathrm{2}} =\frac{\mathrm{sin}\:\alpha}{\mathrm{sin}\:\beta}×{F} \\ $$$$=\frac{\mathrm{2}×\mathrm{5}}{\:\sqrt{\mathrm{5}}×\mathrm{4}}×\mathrm{200}=\mathrm{100}\sqrt{\mathrm{5}}=\mathrm{223}.\mathrm{6}\:{lb} \\ $$
Commented by Eric002 last updated on 02/Mar/21

$${well}\:{done}\:{sir} \\ $$
Commented by ajfour last updated on 02/Mar/21

$${Indeed}. \\ $$
Commented by mr W last updated on 05/Mar/21

$${can}\:{you}\:{consider}\:{solving}\:{Q}\mathrm{134376}\:{sir}? \\ $$
Commented by ajfour last updated on 05/Mar/21

$${sure}\:{i}\:{shall}\:{try}.. \\ $$
Commented by mr W last updated on 07/Mar/21

$${i}\:{have}\:{worked}\:{out}\:{a}\:{solution},\:{but}\:{i}'{m} \\ $$$${not}\:{quite}\:{sure}\:{if}\:{it}'{s}\:{really}\:{correct}. \\ $$$${please}\:{review}. \\ $$
