Question Number 142639 by ajfour last updated on 03/Jun/21
Commented by ajfour last updated on 03/Jun/21
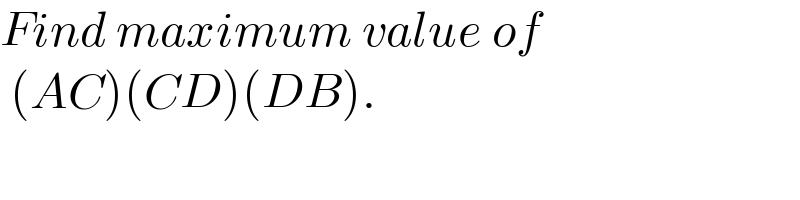
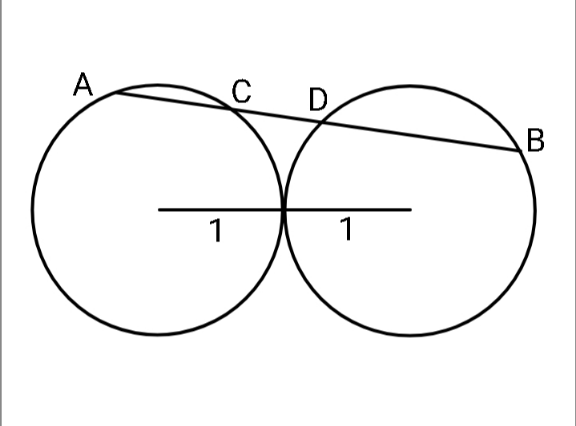
$${Find}\:{maximum}\:{value}\:{of} \\ $$$$\:\left({AC}\right)\left({CD}\right)\left({DB}\right). \\ $$
Commented by mr W last updated on 04/Jun/21
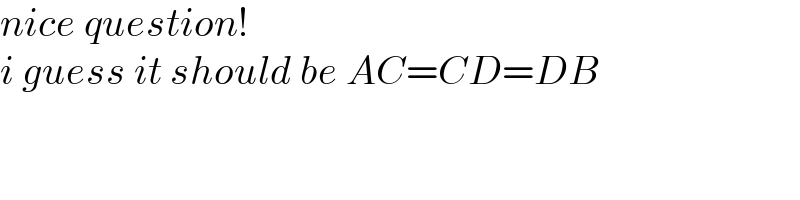
$${nice}\:{question}! \\ $$$${i}\:{guess}\:{it}\:{should}\:{be}\:{AC}={CD}={DB} \\ $$
Answered by 1549442205PVT last updated on 04/Jun/21

Answered by 1549442205PVT last updated on 05/Jun/21

$$\mathrm{Let}\:\mathrm{O},\mathrm{P}\:\mathrm{be}\:\mathrm{the}\:\mathrm{centers}\:\mathrm{of}\:\mathrm{two}\:\mathrm{circles} \\ $$$$\mathrm{Denote}\:\mathrm{by}\:\mathrm{K}\:\mathrm{the}\:\mathrm{projection}\:\mathrm{of}\:\mathrm{O}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{PF}\Rightarrow\mathrm{2}^{\mathrm{2}} =\mathrm{OP}^{\mathrm{2}} =\mathrm{OK}^{\mathrm{2}} +\left(\mathrm{OF}−\mathrm{OE}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{EF}^{\mathrm{2}} =\mathrm{OK}^{\mathrm{2}} =\mathrm{4}−\left(\mathrm{OF}−\mathrm{OE}\right)^{\mathrm{2}} \leqslant\mathrm{4} \\ $$$$\Rightarrow\mathrm{CD}+\frac{\mathrm{AC}+\mathrm{DB}}{\mathrm{2}}\leqslant\mathrm{2}\Rightarrow\mathrm{2CD}+\mathrm{AC}+\mathrm{DB}\leqslant\mathrm{4} \\ $$$$\Rightarrow\mathrm{2CD}.\mathrm{AC}.\mathrm{DB}\leqslant\left(\frac{\mathrm{2CD}+\mathrm{AC}+\mathrm{BD}}{\mathrm{3}}\right)^{\mathrm{3}} \leqslant\frac{\mathrm{64}}{\mathrm{27}} \\ $$$$\Rightarrow\mathrm{CD}.\mathrm{AC}.\mathrm{DB}\leqslant\frac{\mathrm{32}}{\mathrm{27}}.\mathrm{Hence} \\ $$$$\left.\mathrm{AC}.\mathrm{CD}.\mathrm{DB}\right)_{\mathrm{max}} =\frac{\mathrm{32}}{\mathrm{27}} \\ $$$$\mathrm{when}\:\mathrm{CD}=\frac{\mathrm{AC}}{\mathrm{2}}=\frac{\mathrm{BD}}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{3}},\mathrm{OE}=\mathrm{PF}=\frac{\sqrt{\mathrm{5}}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 04/Jun/21

$${nice}\:{solution}\:{sir}! \\ $$
Commented by ajfour last updated on 05/Jun/21
$${Indded},\:{thanks}\:{Sir}. \\ $$
