Menu Close

Question-65589

Tinku Tara
Pin




Question Number 65589 by mr W last updated on 31/Jul/19
Commented by mr W last updated on 31/Jul/19
Answer to Q65277
$${Answer}\:{to}\:{Q}\mathrm{65277} \\ $$
Commented by Tanmay chaudhury last updated on 31/Jul/19
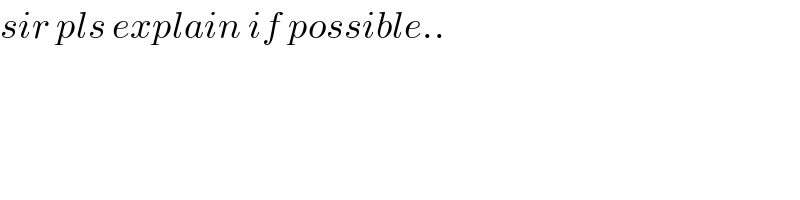
sir pls explain if possible..
$${sir}\:{pls}\:{explain}\:{if}\:{possible}.. \\ $$
Commented by mr W last updated on 12/Feb/21
since the collision is elastic, the velocity of the ball after the collision is the same as before the collision. that means the ball returns to its start position following the same trace as it came. that means also that the direction of the velocity at the point of collision must be perpendicular to the surface. let t=time from A to P t=((R(1+cos α))/(u cos θ)) at point P: v_x =u cos θ v_y =−u sin θ+((gR(1+cos α))/(u cos θ)) v_y =v_x tan α ⇒−u sin θ+((gR(1+cos α))/(u cos θ))=u cos θ tan α ⇒((gR(1+cos α))/(u^2 cos θ))=sin θ+cos θ tan α with λ=((gR)/u^2 ) ⇒((λ(1+cos α))/(cos θ))=sin θ+cos θ tan α ⇒λ=((cos θ(sin θ+cos θ tan α))/(1+cos α)) ⇒(u^2 /(gR))=((1+cos α)/((tan θ+tan α)cos^2 θ)) ...(i) −R sin α=u sin θ t−(1/2)gt^2 ⇒t=((u sin θ+(√(u^2 sin^2 θ+2gR sin α)))/g) ⇒((u sin θ+(√(u^2 sin^2 θ+2gR sin α)))/g)=((R(1+cos α))/(u cos θ)) ⇒sin θ+(√(sin^2 θ+2((gR)/u^2 ) sin α))=((gR)/u^2 )×(((1+cos α))/(cos θ)) ⇒sin θ+(√(sin^2 θ+2λ sin α))=((λ(1+cos α))/(cos θ)) ⇒sin θ+(√(sin^2 θ+2λ sin α))=sin θ+cos θ tan α ⇒(√(sin^2 θ+2λ sin α))=cos θ tan α ⇒sin^2 θ+2λ sin α=(cos θ tan α)^2 ⇒λ=(((cos θ tan α)^2 −sin^2 θ)/(2 sin α)) ⇒(((cos θ tan α)^2 −sin^2 θ)/(2 sin α))=((cos θ(sin θ+cos θ tan α))/(1+cos α)) ⇒((cos θ tan α−sin θ)/(2 sin α))=((cos θ)/(1+cos α)) ⇒(tan α−sin α) cos θ−(1+cos α)sin θ=0 ⇒tan θ=((tan α−sin α)/(1+cos α)) ...(ii) put this into (i): (u^2 /(gR))=(((1+cos α)(1+tan^2 θ))/((tan α+tan θ))) ⇒(u^2 /(gR))=(((1+cos α)^2 +(tan α−sin α)^2 )/(2 tan α)) minimum of u is at: α=64.2057° θ=39.159° u_(min) =0.9098(√(gR))
$${since}\:{the}\:{collision}\:{is}\:{elastic},\:{the} \\ $$$${velocity}\:{of}\:{the}\:{ball}\:{after}\:{the}\:{collision} \\ $$$${is}\:{the}\:{same}\:{as}\:{before}\:{the}\:{collision}. \\ $$$${that}\:{means}\:{the}\:{ball}\:{returns}\:{to}\:{its} \\ $$$${start}\:{position}\:{following}\:{the}\:{same} \\ $$$${trace}\:{as}\:{it}\:{came}.\:{that}\:{means}\:{also} \\ $$$${that}\:{the}\:{direction}\:{of}\:{the}\:{velocity}\:{at}\:{the} \\ $$$${point}\:{of}\:{collision}\:{must}\:{be}\:{perpendicular} \\ $$$${to}\:{the}\:{surface}. \\ $$$$ \\ $$$${let}\:{t}={time}\:{from}\:{A}\:{to}\:{P} \\ $$$${t}=\frac{{R}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}{{u}\:\mathrm{cos}\:\theta} \\ $$$${at}\:{point}\:{P}: \\ $$$${v}_{{x}} ={u}\:\mathrm{cos}\:\theta \\ $$$${v}_{{y}} =−{u}\:\mathrm{sin}\:\theta+\frac{{gR}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}{{u}\:\mathrm{cos}\:\theta} \\ $$$${v}_{{y}} ={v}_{{x}} \mathrm{tan}\:\alpha \\ $$$$\Rightarrow−{u}\:\mathrm{sin}\:\theta+\frac{{gR}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}{{u}\:\mathrm{cos}\:\theta}={u}\:\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\frac{{gR}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}{{u}^{\mathrm{2}} \:\mathrm{cos}\:\theta}=\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha \\ $$$${with}\:\lambda=\frac{{gR}}{{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\lambda\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}{\mathrm{cos}\:\theta}=\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\lambda=\frac{\mathrm{cos}\:\theta\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha\right)}{\mathrm{1}+\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow\frac{{u}^{\mathrm{2}} }{{gR}}=\frac{\mathrm{1}+\mathrm{cos}\:\alpha}{\left(\mathrm{tan}\:\theta+\mathrm{tan}\:\alpha\right)\mathrm{cos}^{\mathrm{2}} \:\theta}\:\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$−{R}\:\mathrm{sin}\:\alpha={u}\:\mathrm{sin}\:\theta\:{t}−\frac{\mathrm{1}}{\mathrm{2}}{gt}^{\mathrm{2}} \\ $$$$\Rightarrow{t}=\frac{{u}\:\mathrm{sin}\:\theta+\sqrt{{u}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}{gR}\:\mathrm{sin}\:\alpha}}{{g}} \\ $$$$\Rightarrow\frac{{u}\:\mathrm{sin}\:\theta+\sqrt{{u}^{\mathrm{2}} \:\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}{gR}\:\mathrm{sin}\:\alpha}}{{g}}=\frac{{R}\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}{{u}\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\mathrm{sin}\:\theta+\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}\frac{{gR}}{{u}^{\mathrm{2}} }\:\mathrm{sin}\:\alpha}=\frac{{gR}}{{u}^{\mathrm{2}} }×\frac{\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\mathrm{sin}\:\theta+\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}\lambda\:\mathrm{sin}\:\alpha}=\frac{\lambda\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)}{\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\mathrm{sin}\:\theta+\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}\lambda\:\mathrm{sin}\:\alpha}=\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\sqrt{\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}\lambda\:\mathrm{sin}\:\alpha}=\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha \\ $$$$\Rightarrow\mathrm{sin}^{\mathrm{2}} \:\theta+\mathrm{2}\lambda\:\mathrm{sin}\:\alpha=\left(\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha\right)^{\mathrm{2}} \\ $$$$\Rightarrow\lambda=\frac{\left(\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha\right)^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{2}\:\mathrm{sin}\:\alpha} \\ $$$$\Rightarrow\frac{\left(\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha\right)^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\theta}{\mathrm{2}\:\mathrm{sin}\:\alpha}=\frac{\mathrm{cos}\:\theta\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha\right)}{\mathrm{1}+\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow\frac{\mathrm{cos}\:\theta\:\mathrm{tan}\:\alpha−\mathrm{sin}\:\theta}{\mathrm{2}\:\mathrm{sin}\:\alpha}=\frac{\mathrm{cos}\:\theta}{\mathrm{1}+\mathrm{cos}\:\alpha} \\ $$$$\Rightarrow\left(\mathrm{tan}\:\alpha−\mathrm{sin}\:\alpha\right)\:\mathrm{cos}\:\theta−\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)\mathrm{sin}\:\theta=\mathrm{0} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{tan}\:\alpha−\mathrm{sin}\:\alpha}{\mathrm{1}+\mathrm{cos}\:\alpha}\:\:\:\:…\left({ii}\right) \\ $$$${put}\:{this}\:{into}\:\left({i}\right): \\ $$$$\frac{{u}^{\mathrm{2}} }{{gR}}=\frac{\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\left(\mathrm{tan}\:\alpha+\mathrm{tan}\:\theta\right)} \\ $$$$\Rightarrow\frac{{u}^{\mathrm{2}} }{{gR}}=\frac{\left(\mathrm{1}+\mathrm{cos}\:\alpha\right)^{\mathrm{2}} +\left(\mathrm{tan}\:\alpha−\mathrm{sin}\:\alpha\right)^{\mathrm{2}} }{\mathrm{2}\:\mathrm{tan}\:\alpha} \\ $$$${minimum}\:{of}\:{u}\:{is}\:{at}: \\ $$$$\alpha=\mathrm{64}.\mathrm{2057}° \\ $$$$\theta=\mathrm{39}.\mathrm{159}° \\ $$$${u}_{{min}} =\mathrm{0}.\mathrm{9098}\sqrt{{gR}} \\ $$
Commented by Tanmay chaudhury last updated on 31/Jul/19
thank you sir...this problem remain unsolved till date...you did it excellent...
$${thank}\:{you}\:{sir}…{this}\:{problem}\:{remain}\:{unsolved} \\ $$$${till}\:{date}…{you}\:{did}\:{it}\:{excellent}… \\ $$
Commented by mr W last updated on 01/Aug/19
Commented by mr W last updated on 01/Aug/19
Commented by mr W last updated on 01/Aug/19
Commented by mr W last updated on 01/Aug/19

Pin