Question Number 65868 by aliesam last updated on 05/Aug/19

Commented by MJS last updated on 05/Aug/19

$$\mathrm{examine}\:\mathrm{the}\:\mathrm{function} \\ $$$${f}\left({x}\right)=\frac{\left(\mathrm{3}{x}−\mathrm{4}\right)\left(\mathrm{5}{x}+\mathrm{4}\right)}{\left(\mathrm{3}{x}−\mathrm{5}\right)\left({x}+\mathrm{5}\right)} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{R}\backslash\left\{−\mathrm{5};\:\frac{\mathrm{5}}{\mathrm{3}}\right\} \\ $$$$\mathrm{local}\:\mathrm{maximum}\:\mathrm{at}\:\begin{pmatrix}{\frac{\mathrm{109}−\sqrt{\mathrm{4921}}}{\mathrm{58}}}\\{\frac{\mathrm{383}−\mathrm{3}\sqrt{\mathrm{4921}}}{\mathrm{200}}}\end{pmatrix}\:\approx\begin{pmatrix}{.\mathrm{67}}\\{.\mathrm{86}}\end{pmatrix} \\ $$$$\mathrm{local}\:\mathrm{minimum}\:\mathrm{at}\:\begin{pmatrix}{\frac{\mathrm{109}+\sqrt{\mathrm{4921}}}{\mathrm{58}}}\\{\frac{\mathrm{383}+\mathrm{3}\sqrt{\mathrm{4921}}}{\mathrm{200}}}\end{pmatrix}\:\approx\begin{pmatrix}{\mathrm{3}.\mathrm{09}}\\{\mathrm{2}.\mathrm{97}}\end{pmatrix} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{try}\:\mathrm{0}<{n}<\frac{\mathrm{5}}{\mathrm{3}}\:\Rightarrow\:{n}=\mathrm{1} \\ $$$$\mathrm{and}\:{n}>\frac{\mathrm{5}}{\mathrm{3}}\:\Rightarrow\:{n}\geqslant\mathrm{2} \\ $$$$\mathrm{but} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{5}\:\Rightarrow\:\mathrm{we}'\mathrm{re}\:\mathrm{looking}\:\mathrm{for}\:{f}\left({x}\right)\in\left\{\mathrm{3};\:\mathrm{4}\right\} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{only}\:\mathrm{solutions}\:\mathrm{are} \\ $$$${n}=\mathrm{2}\:\Rightarrow\:{f}\left({n}\right)=\mathrm{4} \\ $$$${n}=\mathrm{14}\:\Rightarrow\:{f}\left({n}\right)=\mathrm{4} \\ $$
Commented by MJS last updated on 05/Aug/19
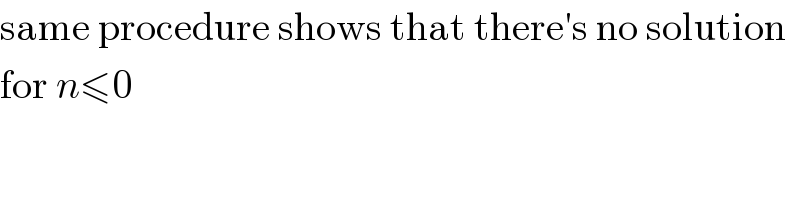
$$\mathrm{same}\:\mathrm{procedure}\:\mathrm{shows}\:\mathrm{that}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{solution} \\ $$$$\mathrm{for}\:{n}\leqslant\mathrm{0} \\ $$
