Question Number 68941 by ahmadshah last updated on 17/Sep/19
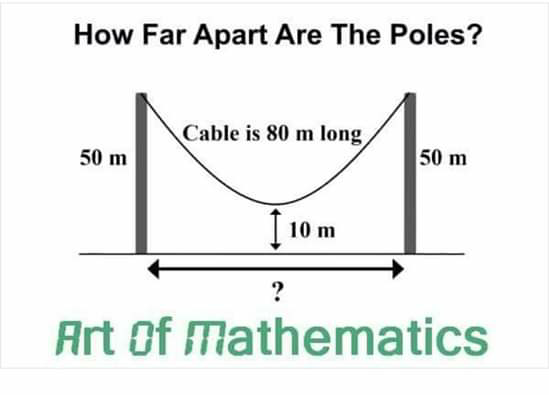
Commented by mr W last updated on 17/Sep/19
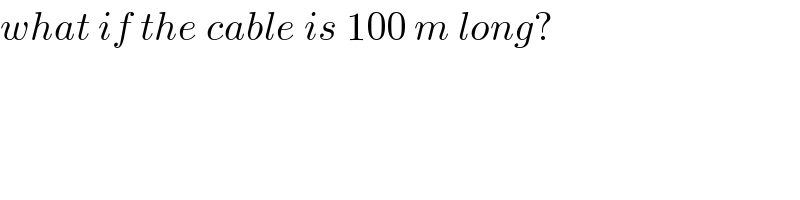
$${what}\:{if}\:{the}\:{cable}\:{is}\:\mathrm{100}\:{m}\:{long}? \\ $$
Commented by MJS last updated on 18/Sep/19
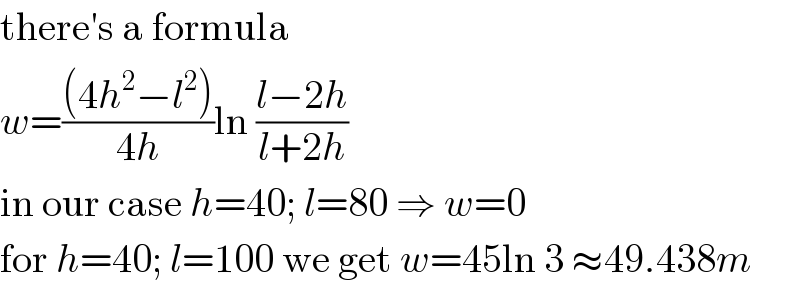
$$\mathrm{there}'\mathrm{s}\:\mathrm{a}\:\mathrm{formula} \\ $$$${w}=\frac{\left(\mathrm{4}{h}^{\mathrm{2}} −{l}^{\mathrm{2}} \right)}{\mathrm{4}{h}}\mathrm{ln}\:\frac{{l}−\mathrm{2}{h}}{{l}+\mathrm{2}{h}} \\ $$$$\mathrm{in}\:\mathrm{our}\:\mathrm{case}\:{h}=\mathrm{40};\:{l}=\mathrm{80}\:\Rightarrow\:{w}=\mathrm{0} \\ $$$$\mathrm{for}\:{h}=\mathrm{40};\:{l}=\mathrm{100}\:\mathrm{we}\:\mathrm{get}\:{w}=\mathrm{45ln}\:\mathrm{3}\:\approx\mathrm{49}.\mathrm{438}{m} \\ $$
Commented by mr W last updated on 18/Sep/19

$${very}\:{right}\:{sir}!\:{thanks}! \\ $$$${i}\:{got}\:{the}\:{formula},\:{see}\:{below}. \\ $$
Answered by ahmadshah last updated on 17/Sep/19
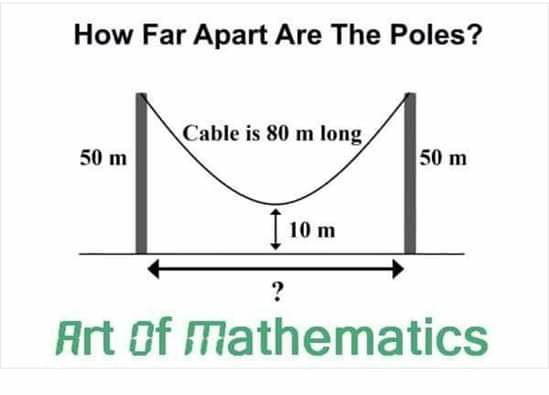
Answered by MJS last updated on 17/Sep/19

$$\mathrm{we}\:\mathrm{had}\:\mathrm{this}\:\mathrm{before} \\ $$$$\mathrm{if}\:\mathrm{the}\:\mathrm{cable}\:\mathrm{is}\:\mathrm{2}{l}\:\mathrm{long}\:\mathrm{and}\:\mathrm{the}\:\mathrm{height}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{curve}\:\mathrm{is}\:{l}\:\Rightarrow\:\mathrm{the}\:\mathrm{distance}\:\mathrm{of}\:\mathrm{the}\:\mathrm{poles}\:=\mathrm{0} \\ $$
Answered by mr W last updated on 18/Sep/19
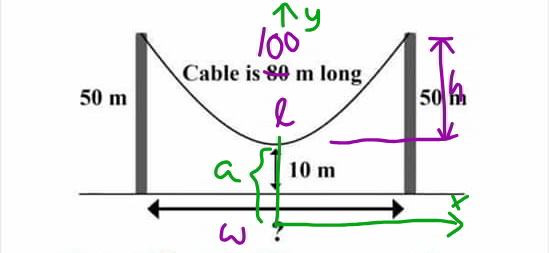
Commented by mr W last updated on 18/Sep/19
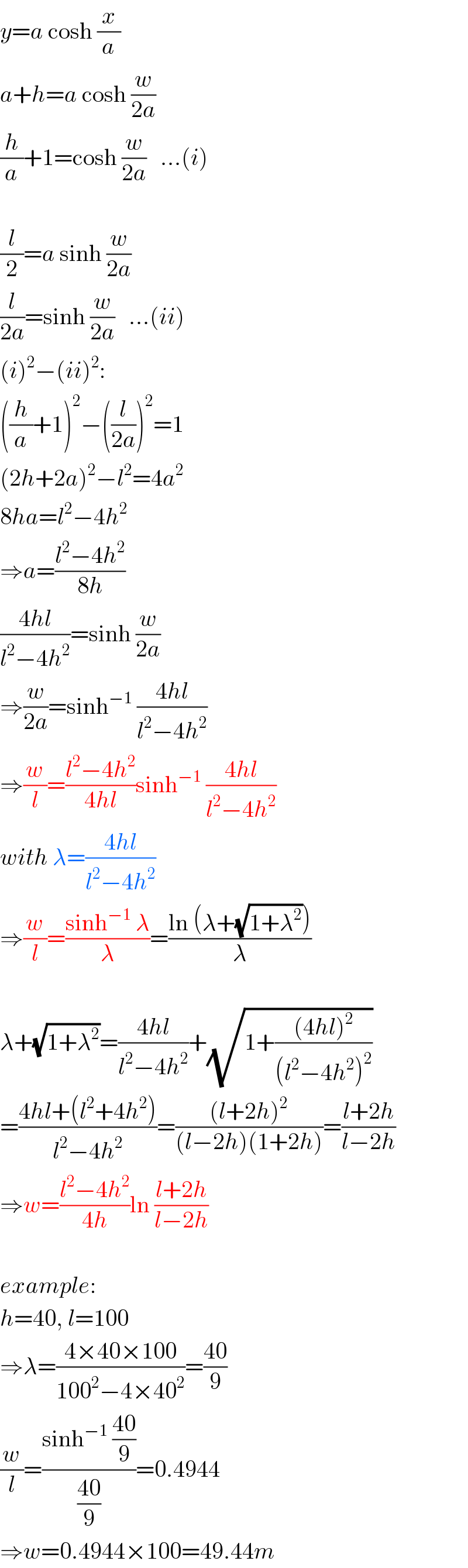
$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${a}+{h}={a}\:\mathrm{cosh}\:\frac{{w}}{\mathrm{2}{a}} \\ $$$$\frac{{h}}{{a}}+\mathrm{1}=\mathrm{cosh}\:\frac{{w}}{\mathrm{2}{a}}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$$\frac{{l}}{\mathrm{2}}={a}\:\mathrm{sinh}\:\frac{{w}}{\mathrm{2}{a}}\: \\ $$$$\frac{{l}}{\mathrm{2}{a}}=\mathrm{sinh}\:\frac{{w}}{\mathrm{2}{a}}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)^{\mathrm{2}} −\left({ii}\right)^{\mathrm{2}} : \\ $$$$\left(\frac{{h}}{{a}}+\mathrm{1}\right)^{\mathrm{2}} −\left(\frac{{l}}{\mathrm{2}{a}}\right)^{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\mathrm{2}{h}+\mathrm{2}{a}\right)^{\mathrm{2}} −{l}^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} \\ $$$$\mathrm{8}{ha}={l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} \\ $$$$\Rightarrow{a}=\frac{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }{\mathrm{8}{h}} \\ $$$$\frac{\mathrm{4}{hl}}{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }=\mathrm{sinh}\:\frac{{w}}{\mathrm{2}{a}} \\ $$$$\Rightarrow\frac{{w}}{\mathrm{2}{a}}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{4}{hl}}{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{w}}{{l}}=\frac{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }{\mathrm{4}{hl}}\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{4}{hl}}{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} } \\ $$$${with}\:\lambda=\frac{\mathrm{4}{hl}}{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{w}}{{l}}=\frac{\mathrm{sinh}^{−\mathrm{1}} \:\lambda}{\lambda}=\frac{\mathrm{ln}\:\left(\lambda+\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }\right)}{\lambda} \\ $$$$ \\ $$$$\lambda+\sqrt{\mathrm{1}+\lambda^{\mathrm{2}} }=\frac{\mathrm{4}{hl}}{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }+\sqrt{\mathrm{1}+\frac{\left(\mathrm{4}{hl}\right)^{\mathrm{2}} }{\left({l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$=\frac{\mathrm{4}{hl}+\left({l}^{\mathrm{2}} +\mathrm{4}{h}^{\mathrm{2}} \right)}{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }=\frac{\left({l}+\mathrm{2}{h}\right)^{\mathrm{2}} }{\left({l}−\mathrm{2}{h}\right)\left(\mathrm{1}+\mathrm{2}{h}\right)}=\frac{{l}+\mathrm{2}{h}}{{l}−\mathrm{2}{h}} \\ $$$$\Rightarrow{w}=\frac{{l}^{\mathrm{2}} −\mathrm{4}{h}^{\mathrm{2}} }{\mathrm{4}{h}}\mathrm{ln}\:\frac{{l}+\mathrm{2}{h}}{{l}−\mathrm{2}{h}} \\ $$$$ \\ $$$${example}: \\ $$$${h}=\mathrm{40},\:{l}=\mathrm{100} \\ $$$$\Rightarrow\lambda=\frac{\mathrm{4}×\mathrm{40}×\mathrm{100}}{\mathrm{100}^{\mathrm{2}} −\mathrm{4}×\mathrm{40}^{\mathrm{2}} }=\frac{\mathrm{40}}{\mathrm{9}} \\ $$$$\frac{{w}}{{l}}=\frac{\mathrm{sinh}^{−\mathrm{1}} \:\frac{\mathrm{40}}{\mathrm{9}}}{\frac{\mathrm{40}}{\mathrm{9}}}=\mathrm{0}.\mathrm{4944} \\ $$$$\Rightarrow{w}=\mathrm{0}.\mathrm{4944}×\mathrm{100}=\mathrm{49}.\mathrm{44}{m} \\ $$
Commented by MJS last updated on 19/Sep/19

$$\mathrm{great}! \\ $$
