Question Number 76443 by aliesam last updated on 27/Dec/19

Answered by mr W last updated on 27/Dec/19
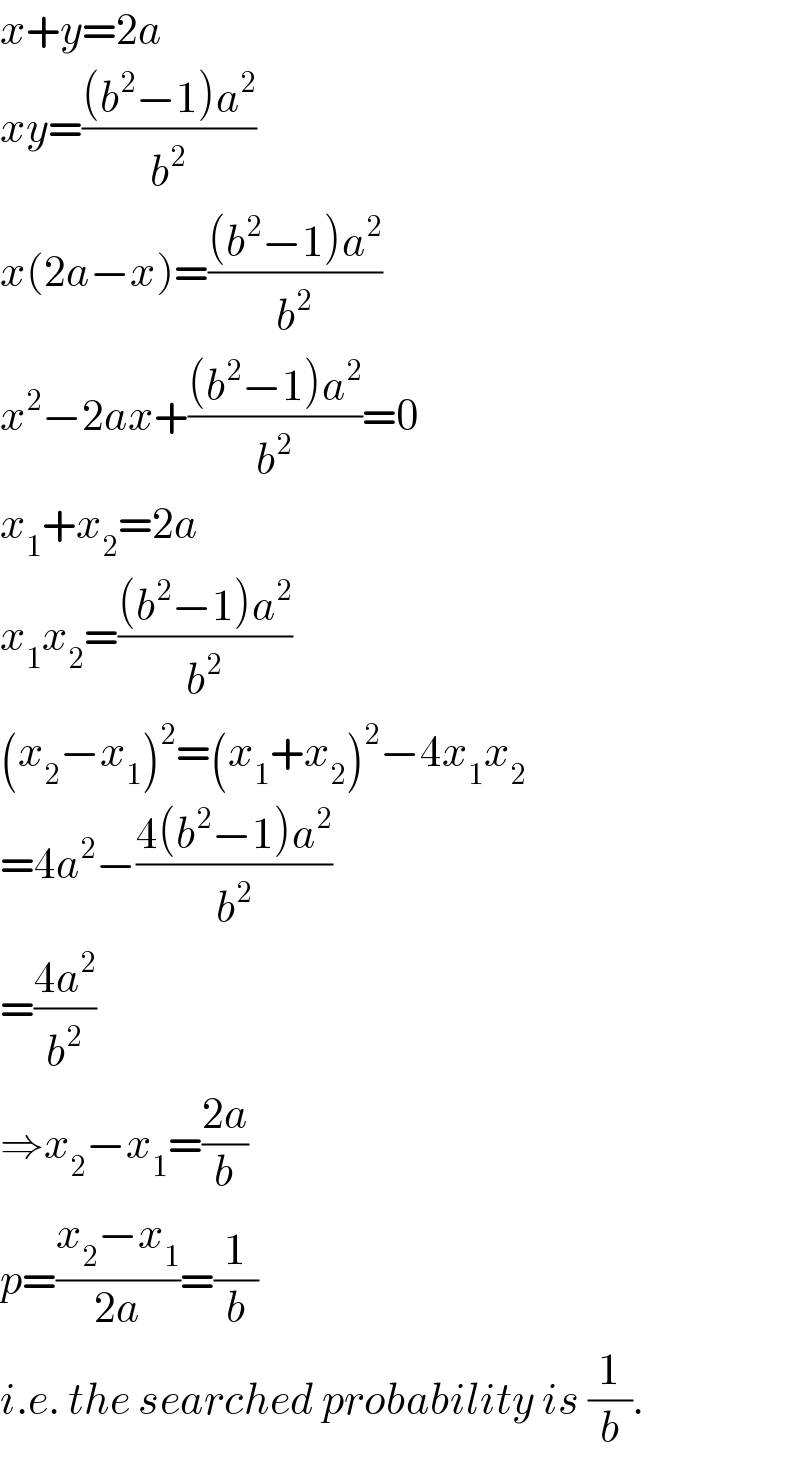
$${x}+{y}=\mathrm{2}{a} \\ $$$${xy}=\frac{\left({b}^{\mathrm{2}} −\mathrm{1}\right){a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$${x}\left(\mathrm{2}{a}−{x}\right)=\frac{\left({b}^{\mathrm{2}} −\mathrm{1}\right){a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} −\mathrm{2}{ax}+\frac{\left({b}^{\mathrm{2}} −\mathrm{1}\right){a}^{\mathrm{2}} }{{b}^{\mathrm{2}} }=\mathrm{0} \\ $$$${x}_{\mathrm{1}} +{x}_{\mathrm{2}} =\mathrm{2}{a} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} =\frac{\left({b}^{\mathrm{2}} −\mathrm{1}\right){a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} =\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4}{x}_{\mathrm{1}} {x}_{\mathrm{2}} \\ $$$$=\mathrm{4}{a}^{\mathrm{2}} −\frac{\mathrm{4}\left({b}^{\mathrm{2}} −\mathrm{1}\right){a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}_{\mathrm{2}} −{x}_{\mathrm{1}} =\frac{\mathrm{2}{a}}{{b}} \\ $$$${p}=\frac{{x}_{\mathrm{2}} −{x}_{\mathrm{1}} }{\mathrm{2}{a}}=\frac{\mathrm{1}}{{b}} \\ $$$${i}.{e}.\:{the}\:{searched}\:{probability}\:{is}\:\frac{\mathrm{1}}{{b}}. \\ $$
