Question-76855

Question Number 76855 by aliesam last updated on 31/Dec/19

Commented by aliesam last updated on 31/Dec/19

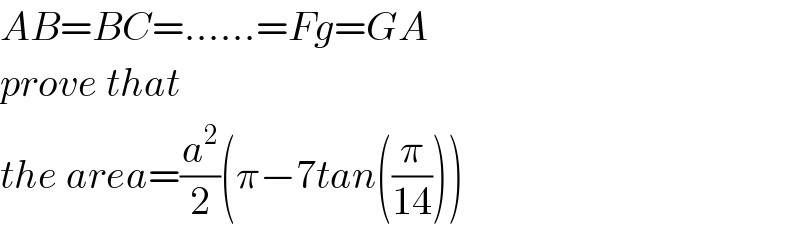
AB=BC=......=Fg=GA prove that the area=(a^2 /2)(π−7tan((π/(14))))

$${AB}={BC}=……={Fg}={GA} \\ $$$${prove}\:{that}\: \\ $$$${the}\:{area}=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\pi−\mathrm{7}{tan}\left(\frac{\pi}{\mathrm{14}}\right)\right) \\ $$

Commented by 67549972 last updated on 08/Feb/20

$$ \\ $$

Answered by mr W last updated on 31/Dec/19

Commented by mr W last updated on 31/Dec/19

2θ=((2π)/7) ⇒θ=(π/7) R cos (θ/2)=(a/2) ⇒R=(a/(2 cos (π/(14)))) A_(blue) =((R^2 sin 2θ)/2)=((a^2 sin ((2π)/7))/(8 cos^2 (π/(14)))) A_(green) =(a^2 /2)(θ−sin θ)=(a^2 /2)((π/7)−sin (π/7)) A=7(A_(blue) +A_(green) ) =7[((a^2 sin ((2π)/7))/(8 cos^2 (π/(14))))+(a^2 /2)((π/7)−sin (π/7))] =(a^2 /2)[π+((7 sin ((2π)/7))/(4 cos^2 (π/(14))))−7 sin (π/7)] =(a^2 /2)[π+((7 sin (π/7) cos (π/7))/(2 cos^2 (π/(14))))−7 sin (π/7)] =(a^2 /2)[π+7 sin (π/7)(((cos (π/7))/(2 cos^2 (π/(14))))−1)] =(a^2 /2)[π+7 sin (π/7)(((cos (π/7)−2 cos^2 (π/(14)))/(2 cos^2 (π/(14)))))] =(a^2 /2)[π−((7 sin (π/7))/(2 cos^2 (π/(14))))] =(a^2 /2)[π−((14 sin (π/(14)) cos (π/(14)))/(2 cos^2 (π/(14))))] =(a^2 /2)[π−((7 sin (π/(14)))/(cos (π/(14))))] =(a^2 /2)(π−7 tan (π/(14)))

$$\mathrm{2}\theta=\frac{\mathrm{2}\pi}{\mathrm{7}} \\ $$$$\Rightarrow\theta=\frac{\pi}{\mathrm{7}} \\ $$$${R}\:\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\frac{{a}}{\mathrm{2}} \\ $$$$\Rightarrow{R}=\frac{{a}}{\mathrm{2}\:\mathrm{cos}\:\frac{\pi}{\mathrm{14}}} \\ $$$${A}_{{blue}} =\frac{{R}^{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} \:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{7}}}{\mathrm{8}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}} \\ $$$${A}_{{green}} =\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\theta−\mathrm{sin}\:\theta\right)=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{7}}−\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\right) \\ $$$$ \\ $$$${A}=\mathrm{7}\left({A}_{{blue}} +{A}_{{green}} \right) \\ $$$$=\mathrm{7}\left[\frac{{a}^{\mathrm{2}} \:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{7}}}{\mathrm{8}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}}+\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{7}}−\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\right)\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\pi+\frac{\mathrm{7}\:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{7}}}{\mathrm{4}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}}−\mathrm{7}\:\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\pi+\frac{\mathrm{7}\:\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\:\mathrm{cos}\:\frac{\pi}{\mathrm{7}}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}}−\mathrm{7}\:\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\pi+\mathrm{7}\:\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\left(\frac{\mathrm{cos}\:\frac{\pi}{\mathrm{7}}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}}−\mathrm{1}\right)\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\pi+\mathrm{7}\:\mathrm{sin}\:\frac{\pi}{\mathrm{7}}\left(\frac{\mathrm{cos}\:\frac{\pi}{\mathrm{7}}−\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}}\right)\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\pi−\frac{\mathrm{7}\:\mathrm{sin}\:\frac{\pi}{\mathrm{7}}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}}\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\pi−\frac{\mathrm{14}\:\mathrm{sin}\:\frac{\pi}{\mathrm{14}}\:\mathrm{cos}\:\frac{\pi}{\mathrm{14}}}{\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{14}}}\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left[\pi−\frac{\mathrm{7}\:\mathrm{sin}\:\frac{\pi}{\mathrm{14}}}{\mathrm{cos}\:\frac{\pi}{\mathrm{14}}}\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{2}}\left(\pi−\mathrm{7}\:\mathrm{tan}\:\frac{\pi}{\mathrm{14}}\right) \\ $$

Commented by jagoll last updated on 31/Dec/19