Question Number 77132 by peter frank last updated on 03/Jan/20

Commented by kaivan.ahmadi last updated on 03/Jan/20
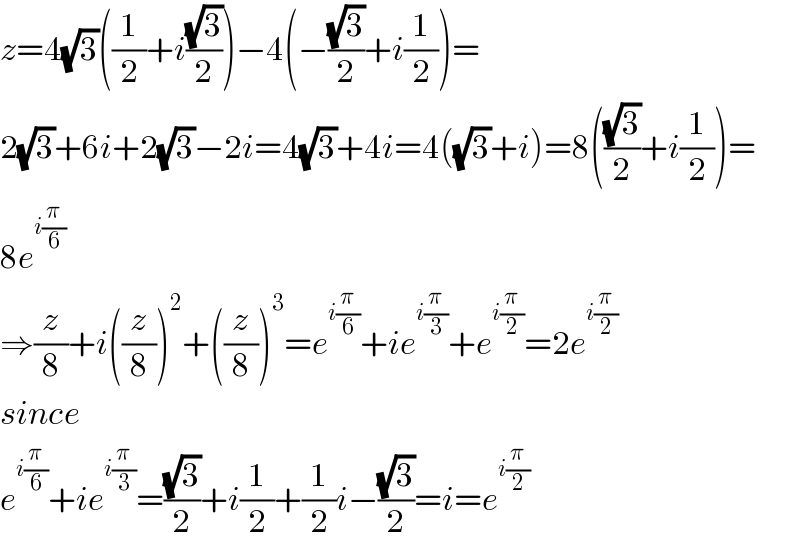
$${z}=\mathrm{4}\sqrt{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)−\mathrm{4}\left(−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+{i}\frac{\mathrm{1}}{\mathrm{2}}\right)= \\ $$$$\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{6}{i}+\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{2}{i}=\mathrm{4}\sqrt{\mathrm{3}}+\mathrm{4}{i}=\mathrm{4}\left(\sqrt{\mathrm{3}}+{i}\right)=\mathrm{8}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+{i}\frac{\mathrm{1}}{\mathrm{2}}\right)= \\ $$$$\mathrm{8}{e}^{{i}\frac{\pi}{\mathrm{6}}} \\ $$$$\Rightarrow\frac{{z}}{\mathrm{8}}+{i}\left(\frac{{z}}{\mathrm{8}}\right)^{\mathrm{2}} +\left(\frac{{z}}{\mathrm{8}}\right)^{\mathrm{3}} ={e}^{{i}\frac{\pi}{\mathrm{6}}} +{ie}^{{i}\frac{\pi}{\mathrm{3}}} +{e}^{{i}\frac{\pi}{\mathrm{2}}} =\mathrm{2}{e}^{{i}\frac{\pi}{\mathrm{2}}} \\ $$$${since} \\ $$$${e}^{{i}\frac{\pi}{\mathrm{6}}} +{ie}^{{i}\frac{\pi}{\mathrm{3}}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+{i}\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{i}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}={i}={e}^{{i}\frac{\pi}{\mathrm{2}}} \\ $$
