Question-77229

Question Number 77229 by Maclaurin Stickker last updated on 04/Jan/20

Commented by Maclaurin Stickker last updated on 04/Jan/20

$${ABC}\:{is}\:{a}\:{triangle}.\:{Radius}\:{circumferences} \\ $$$${shown}\:{in}\:{the}\:{figure}\:{are}\:{drawn} \\ $$$${internally}\:{to}\:{the}\:{triangle}\:{tanging} \\ $$$${two}\:{of}\:{its}\:{sides}\:{and}\:{the}\:{incircle}. \\ $$$${Determine}\:{the}\:{radius}\:{of}\:{the}\:{incircle}. \\ $$$$ \\ $$

Answered by mr W last updated on 04/Jan/20

Commented by mr W last updated on 05/Jan/20

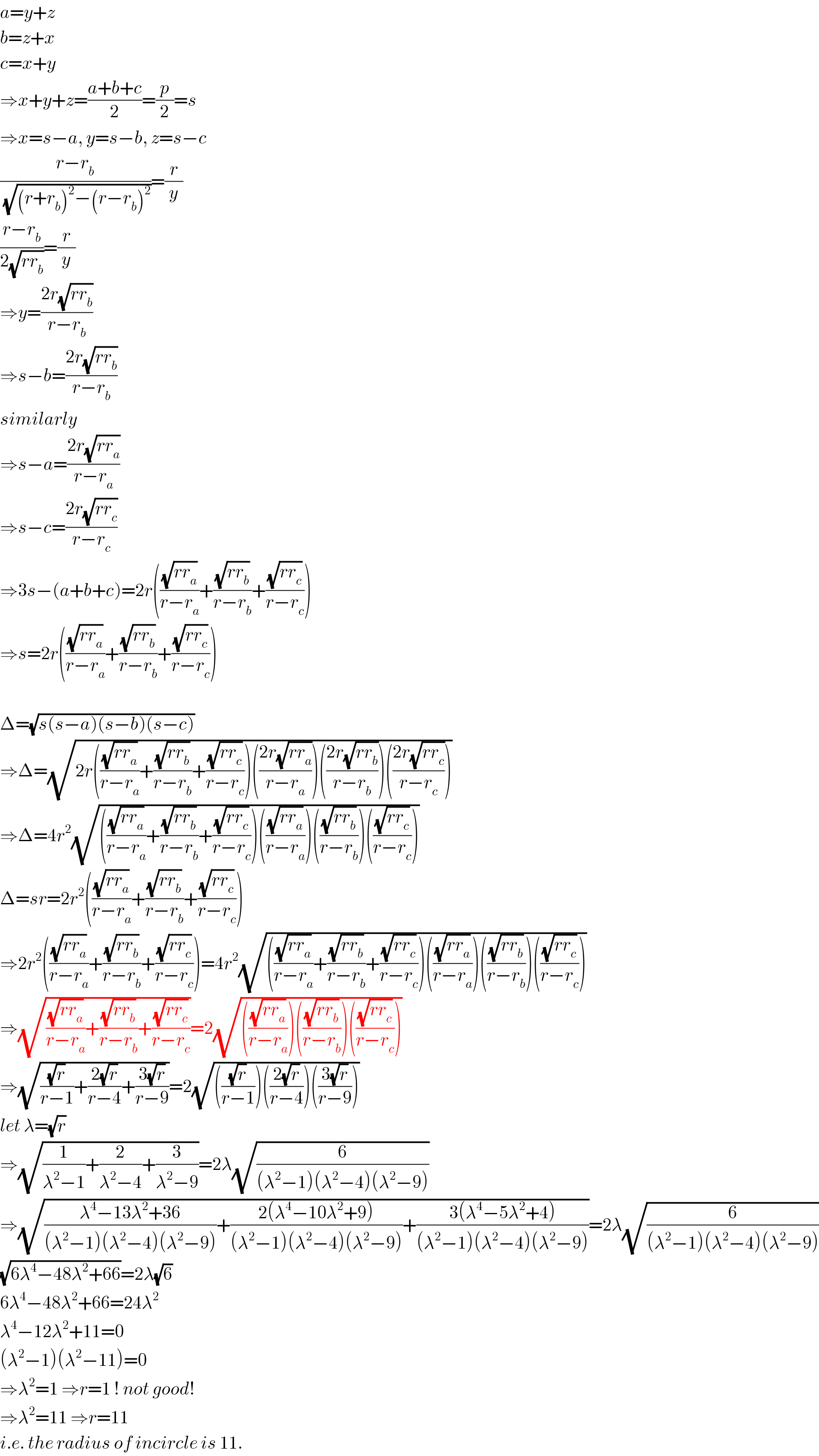
a=y+z b=z+x c=x+y ⇒x+y+z=((a+b+c)/2)=(p/2)=s ⇒x=s−a, y=s−b, z=s−c ((r−r_b )/( (√((r+r_b )^2 −(r−r_b )^2 ))))=(r/y) ((r−r_b )/(2(√(rr_b ))))=(r/y) ⇒y=((2r(√(rr_b )))/(r−r_b )) ⇒s−b=((2r(√(rr_b )))/(r−r_b )) similarly ⇒s−a=((2r(√(rr_a )))/(r−r_a )) ⇒s−c=((2r(√(rr_c )))/(r−r_c )) ⇒3s−(a+b+c)=2r(((√(rr_a ))/(r−r_a ))+((√(rr_b ))/(r−r_b ))+((√(rr_c ))/(r−r_c ))) ⇒s=2r(((√(rr_a ))/(r−r_a ))+((√(rr_b ))/(r−r_b ))+((√(rr_c ))/(r−r_c ))) Δ=(√(s(s−a)(s−b)(s−c))) ⇒Δ=(√(2r(((√(rr_a ))/(r−r_a ))+((√(rr_b ))/(r−r_b ))+((√(rr_c ))/(r−r_c )))(((2r(√(rr_a )))/(r−r_a )))(((2r(√(rr_b )))/(r−r_b )))(((2r(√(rr_c )))/(r−r_c ))))) ⇒Δ=4r^2 (√((((√(rr_a ))/(r−r_a ))+((√(rr_b ))/(r−r_b ))+((√(rr_c ))/(r−r_c )))(((√(rr_a ))/(r−r_a )))(((√(rr_b ))/(r−r_b )))(((√(rr_c ))/(r−r_c ))))) Δ=sr=2r^2 (((√(rr_a ))/(r−r_a ))+((√(rr_b ))/(r−r_b ))+((√(rr_c ))/(r−r_c ))) ⇒2r^2 (((√(rr_a ))/(r−r_a ))+((√(rr_b ))/(r−r_b ))+((√(rr_c ))/(r−r_c )))=4r^2 (√((((√(rr_a ))/(r−r_a ))+((√(rr_b ))/(r−r_b ))+((√(rr_c ))/(r−r_c )))(((√(rr_a ))/(r−r_a )))(((√(rr_b ))/(r−r_b )))(((√(rr_c ))/(r−r_c ))))) ⇒(√(((√(rr_a ))/(r−r_a ))+((√(rr_b ))/(r−r_b ))+((√(rr_c ))/(r−r_c ))))=2(√((((√(rr_a ))/(r−r_a )))(((√(rr_b ))/(r−r_b )))(((√(rr_c ))/(r−r_c ))))) ⇒(√(((√r)/(r−1))+((2(√r))/(r−4))+((3(√r))/(r−9))))=2(√((((√r)/(r−1)))(((2(√r))/(r−4)))(((3(√r))/(r−9))))) let λ=(√r) ⇒(√((1/(λ^2 −1))+(2/(λ^2 −4))+(3/(λ^2 −9))))=2λ(√(6/((λ^2 −1)(λ^2 −4)(λ^2 −9)))) ⇒(√(((λ^4 −13λ^2 +36)/((λ^2 −1)(λ^2 −4)(λ^2 −9)))+((2(λ^4 −10λ^2 +9))/((λ^2 −1)(λ^2 −4)(λ^2 −9)))+((3(λ^4 −5λ^2 +4))/((λ^2 −1)(λ^2 −4)(λ^2 −9)))))=2λ(√(6/((λ^2 −1)(λ^2 −4)(λ^2 −9)))) (√(6λ^4 −48λ^2 +66))=2λ(√6) 6λ^4 −48λ^2 +66=24λ^2 λ^4 −12λ^2 +11=0 (λ^2 −1)(λ^2 −11)=0 ⇒λ^2 =1 ⇒r=1 ! not good! ⇒λ^2 =11 ⇒r=11 i.e. the radius of incircle is 11.

$${a}={y}+{z} \\ $$$${b}={z}+{x} \\ $$$${c}={x}+{y} \\ $$$$\Rightarrow{x}+{y}+{z}=\frac{{a}+{b}+{c}}{\mathrm{2}}=\frac{{p}}{\mathrm{2}}={s} \\ $$$$\Rightarrow{x}={s}−{a},\:{y}={s}−{b},\:{z}={s}−{c} \\ $$$$\frac{{r}−{r}_{{b}} }{\:\sqrt{\left({r}+{r}_{{b}} \right)^{\mathrm{2}} −\left({r}−{r}_{{b}} \right)^{\mathrm{2}} }}=\frac{{r}}{{y}} \\ $$$$\frac{{r}−{r}_{{b}} }{\mathrm{2}\sqrt{{rr}_{{b}} }}=\frac{{r}}{{y}} \\ $$$$\Rightarrow{y}=\frac{\mathrm{2}{r}\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} } \\ $$$$\Rightarrow{s}−{b}=\frac{\mathrm{2}{r}\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} } \\ $$$${similarly} \\ $$$$\Rightarrow{s}−{a}=\frac{\mathrm{2}{r}\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} } \\ $$$$\Rightarrow{s}−{c}=\frac{\mathrm{2}{r}\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} } \\ $$$$\Rightarrow\mathrm{3}{s}−\left({a}+{b}+{c}\right)=\mathrm{2}{r}\left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }+\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }+\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right) \\ $$$$\Rightarrow{s}=\mathrm{2}{r}\left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }+\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }+\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right) \\ $$$$ \\ $$$$\Delta=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$$\Rightarrow\Delta=\sqrt{\mathrm{2}{r}\left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }+\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }+\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right)\left(\frac{\mathrm{2}{r}\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }\right)\left(\frac{\mathrm{2}{r}\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }\right)\left(\frac{\mathrm{2}{r}\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right)} \\ $$$$\Rightarrow\Delta=\mathrm{4}{r}^{\mathrm{2}} \sqrt{\left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }+\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }+\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right)\left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }\right)\left(\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }\right)\left(\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right)} \\ $$$$\Delta={sr}=\mathrm{2}{r}^{\mathrm{2}} \left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }+\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }+\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right) \\ $$$$\Rightarrow\mathrm{2}{r}^{\mathrm{2}} \left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }+\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }+\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right)=\mathrm{4}{r}^{\mathrm{2}} \sqrt{\left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }+\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }+\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right)\left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }\right)\left(\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }\right)\left(\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right)} \\ $$$$\Rightarrow\sqrt{\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }+\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }+\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }}=\mathrm{2}\sqrt{\left(\frac{\sqrt{{rr}_{{a}} }}{{r}−{r}_{{a}} }\right)\left(\frac{\sqrt{{rr}_{{b}} }}{{r}−{r}_{{b}} }\right)\left(\frac{\sqrt{{rr}_{{c}} }}{{r}−{r}_{{c}} }\right)} \\ $$$$\Rightarrow\sqrt{\frac{\sqrt{{r}}}{{r}−\mathrm{1}}+\frac{\mathrm{2}\sqrt{{r}}}{{r}−\mathrm{4}}+\frac{\mathrm{3}\sqrt{{r}}}{{r}−\mathrm{9}}}=\mathrm{2}\sqrt{\left(\frac{\sqrt{{r}}}{{r}−\mathrm{1}}\right)\left(\frac{\mathrm{2}\sqrt{{r}}}{{r}−\mathrm{4}}\right)\left(\frac{\mathrm{3}\sqrt{{r}}}{{r}−\mathrm{9}}\right)} \\ $$$${let}\:\lambda=\sqrt{{r}} \\ $$$$\Rightarrow\sqrt{\frac{\mathrm{1}}{\lambda^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{2}}{\lambda^{\mathrm{2}} −\mathrm{4}}+\frac{\mathrm{3}}{\lambda^{\mathrm{2}} −\mathrm{9}}}=\mathrm{2}\lambda\sqrt{\frac{\mathrm{6}}{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\mathrm{4}\right)\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)}} \\ $$$$\Rightarrow\sqrt{\frac{\lambda^{\mathrm{4}} −\mathrm{13}\lambda^{\mathrm{2}} +\mathrm{36}}{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\mathrm{4}\right)\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)}+\frac{\mathrm{2}\left(\lambda^{\mathrm{4}} −\mathrm{10}\lambda^{\mathrm{2}} +\mathrm{9}\right)}{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\mathrm{4}\right)\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)}+\frac{\mathrm{3}\left(\lambda^{\mathrm{4}} −\mathrm{5}\lambda^{\mathrm{2}} +\mathrm{4}\right)}{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\mathrm{4}\right)\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)}}=\mathrm{2}\lambda\sqrt{\frac{\mathrm{6}}{\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\mathrm{4}\right)\left(\lambda^{\mathrm{2}} −\mathrm{9}\right)}} \\ $$$$\sqrt{\mathrm{6}\lambda^{\mathrm{4}} −\mathrm{48}\lambda^{\mathrm{2}} +\mathrm{66}}=\mathrm{2}\lambda\sqrt{\mathrm{6}} \\ $$$$\mathrm{6}\lambda^{\mathrm{4}} −\mathrm{48}\lambda^{\mathrm{2}} +\mathrm{66}=\mathrm{24}\lambda^{\mathrm{2}} \\ $$$$\lambda^{\mathrm{4}} −\mathrm{12}\lambda^{\mathrm{2}} +\mathrm{11}=\mathrm{0} \\ $$$$\left(\lambda^{\mathrm{2}} −\mathrm{1}\right)\left(\lambda^{\mathrm{2}} −\mathrm{11}\right)=\mathrm{0} \\ $$$$\Rightarrow\lambda^{\mathrm{2}} =\mathrm{1}\:\Rightarrow{r}=\mathrm{1}\:!\:{not}\:{good}! \\ $$$$\Rightarrow\lambda^{\mathrm{2}} =\mathrm{11}\:\Rightarrow{r}=\mathrm{11} \\ $$$${i}.{e}.\:{the}\:{radius}\:{of}\:{incircle}\:{is}\:\mathrm{11}. \\ $$

Commented by Maclaurin Stickker last updated on 04/Jan/20

$${wow}!\:{perfect}\centerdot \\ $$

Commented by mr W last updated on 04/Jan/20

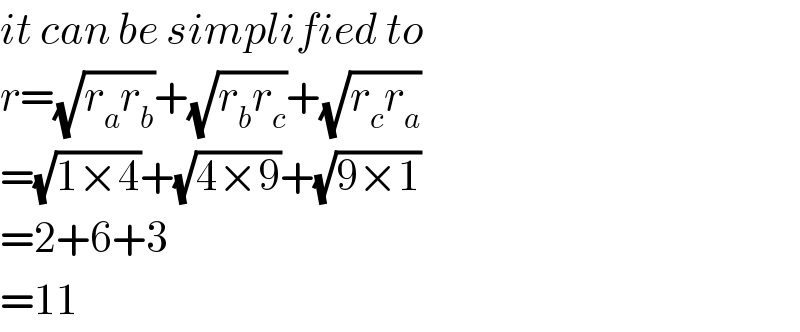
it can be simplified to r=(√(r_a r_b ))+(√(r_b r_c ))+(√(r_c r_a )) =(√(1×4))+(√(4×9))+(√(9×1)) =2+6+3 =11

$${it}\:{can}\:{be}\:{simplified}\:{to} \\ $$$${r}=\sqrt{{r}_{{a}} {r}_{{b}} }+\sqrt{{r}_{{b}} {r}_{{c}} }+\sqrt{{r}_{{c}} {r}_{{a}} } \\ $$$$=\sqrt{\mathrm{1}×\mathrm{4}}+\sqrt{\mathrm{4}×\mathrm{9}}+\sqrt{\mathrm{9}×\mathrm{1}} \\ $$$$=\mathrm{2}+\mathrm{6}+\mathrm{3} \\ $$$$=\mathrm{11} \\ $$

Commented by otchereabdullai@gmail.com last updated on 04/Jan/20