Menu Close

real-analysis-prove-0-1-ln-ln-1-x-ln-2-x-dx-3-2-

Tinku Tara
Pin




Question Number 131227 by mnjuly1970 last updated on 02/Feb/21
... real analysis ... prove:: 𝛀= ∫_0 ^( 1) ln(ln((1/x)))ln^2 (x)dx=3−2γ
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:…\:{real}\:\:{analysis}\:… \\ $$$$\:\:\:\:\:\:{prove}:: \\ $$$$\:\:\:\boldsymbol{\Omega}=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {ln}\left({ln}\left(\frac{\mathrm{1}}{{x}}\right)\right){ln}^{\mathrm{2}} \left({x}\right){dx}=\mathrm{3}−\mathrm{2}\gamma \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 02/Feb/21
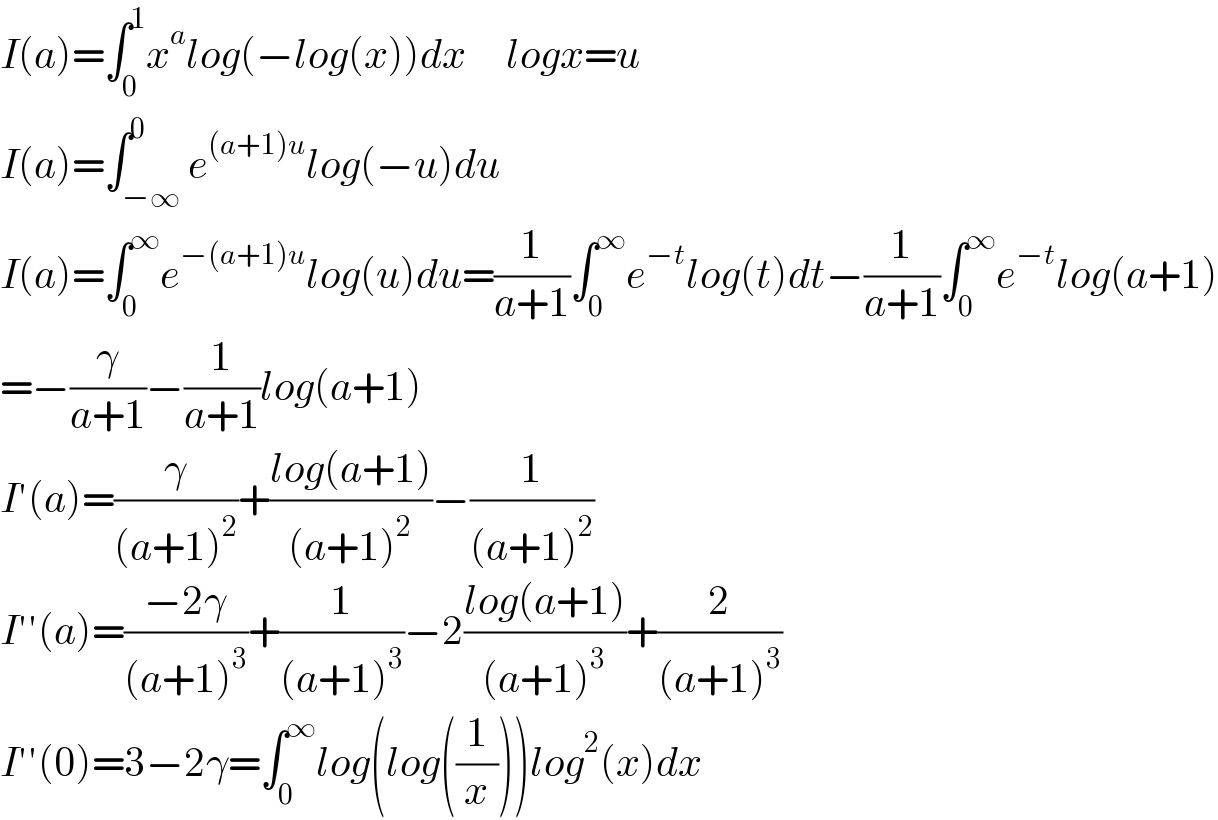
I(a)=∫_0 ^1 x^a log(−log(x))dx logx=u I(a)=∫_(−∞) ^0 e^((a+1)u) log(−u)du I(a)=∫_0 ^∞ e^(−(a+1)u) log(u)du=(1/(a+1))∫_0 ^∞ e^(−t) log(t)dt−(1/(a+1))∫_0 ^∞ e^(−t) log(a+1) =−(γ/(a+1))−(1/(a+1))log(a+1) I′(a)=(γ/((a+1)^2 ))+((log(a+1))/((a+1)^2 ))−(1/((a+1)^2 )) I′′(a)=((−2γ)/((a+1)^3 ))+(1/((a+1)^3 ))−2((log(a+1))/((a+1)^3 ))+(2/((a+1)^3 )) I′′(0)=3−2γ=∫_0 ^∞ log(log((1/x)))log^2 (x)dx
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} {log}\left(−{log}\left({x}\right)\right){dx}\:\:\:\:\:{logx}={u} \\ $$$${I}\left({a}\right)=\int_{−\infty} ^{\mathrm{0}} {e}^{\left({a}+\mathrm{1}\right){u}} {log}\left(−{u}\right){du} \\ $$$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−\left({a}+\mathrm{1}\right){u}} {log}\left({u}\right){du}=\frac{\mathrm{1}}{{a}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {log}\left({t}\right){dt}−\frac{\mathrm{1}}{{a}+\mathrm{1}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} {log}\left({a}+\mathrm{1}\right) \\ $$$$=−\frac{\gamma}{{a}+\mathrm{1}}−\frac{\mathrm{1}}{{a}+\mathrm{1}}{log}\left({a}+\mathrm{1}\right) \\ $$$${I}'\left({a}\right)=\frac{\gamma}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{log}\left({a}+\mathrm{1}\right)}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${I}''\left({a}\right)=\frac{−\mathrm{2}\gamma}{\left({a}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\left({a}+\mathrm{1}\right)^{\mathrm{3}} }−\mathrm{2}\frac{{log}\left({a}+\mathrm{1}\right)}{\left({a}+\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{2}}{\left({a}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$${I}''\left(\mathrm{0}\right)=\mathrm{3}−\mathrm{2}\gamma=\int_{\mathrm{0}} ^{\infty} {log}\left({log}\left(\frac{\mathrm{1}}{{x}}\right)\right){log}^{\mathrm{2}} \left({x}\right){dx} \\ $$
Commented by mnjuly1970 last updated on 02/Feb/21
thank you mr dwaipayan...
$${thank}\:{you}\:{mr}\:{dwaipayan}… \\ $$

Pin