Question Number 11302 by uni last updated on 19/Mar/17
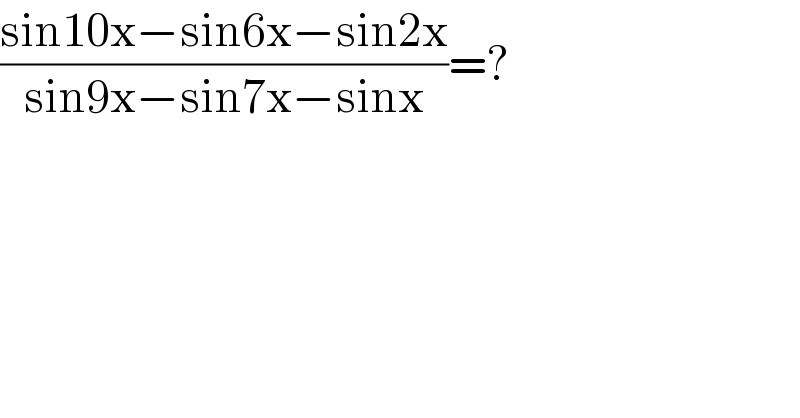
$$\frac{\mathrm{sin10x}−\mathrm{sin6x}−\mathrm{sin2x}}{\mathrm{sin9x}−\mathrm{sin7x}−\mathrm{sinx}}=? \\ $$
Answered by sandy_suhendra last updated on 20/Mar/17
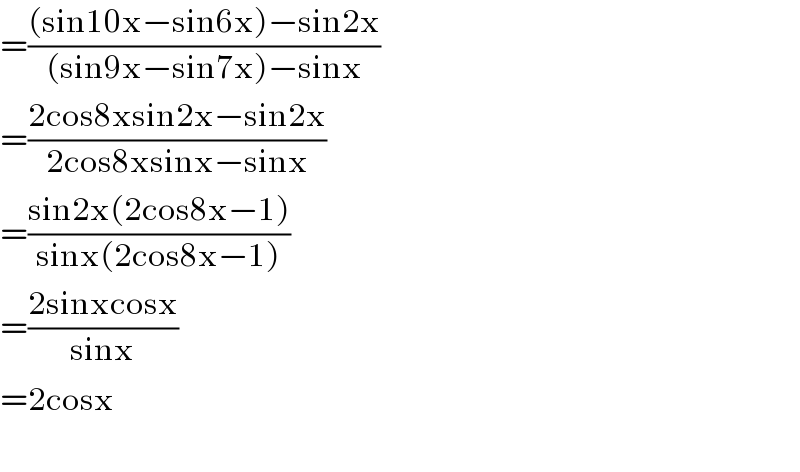
$$=\frac{\left(\mathrm{sin10x}−\mathrm{sin6x}\right)−\mathrm{sin2x}}{\left(\mathrm{sin9x}−\mathrm{sin7x}\right)−\mathrm{sinx}} \\ $$$$=\frac{\mathrm{2cos8xsin2x}−\mathrm{sin2x}}{\mathrm{2cos8xsinx}−\mathrm{sinx}} \\ $$$$=\frac{\mathrm{sin2x}\left(\mathrm{2cos8x}−\mathrm{1}\right)}{\mathrm{sinx}\left(\mathrm{2cos8x}−\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{2sinxcosx}}{\mathrm{sinx}} \\ $$$$=\mathrm{2cosx} \\ $$$$ \\ $$
Answered by sm3l2996 last updated on 20/Mar/17
![I=((sin(10x)−sin(6x)−sin(2x))/(sin(9x)−sin(7x)−sin(x))) =((sin(8x)cos(2x)+sin(2x)cos(8x)−[sin(8x)cos(2x)−sin(2x)cos(8x)]−sin(2x))/(sin(8x)cos(x)+sin(x)cos(8x)−[sin(8x)cos(x)−sin(x)cos(8x)]−sin(x))) =((2sin(2x)cos(8x)−sin(2x))/(2sin(x)cos(8x)−sin(x)))=((sin(2x)[2cos(8x)−1])/(sin(x)[2cos(8x)−1]))=((2sin(x)cos(x))/(sin(x))) I=2cos(x)](https://www.tinkutara.com/question/Q11306.png)
$$\mathrm{I}=\frac{\mathrm{sin}\left(\mathrm{10x}\right)−\mathrm{sin}\left(\mathrm{6x}\right)−\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{sin}\left(\mathrm{9x}\right)−\mathrm{sin}\left(\mathrm{7x}\right)−\mathrm{sin}\left(\mathrm{x}\right)} \\ $$$$=\frac{\mathrm{sin}\left(\mathrm{8x}\right)\mathrm{cos}\left(\mathrm{2x}\right)+\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{8x}\right)−\left[\mathrm{sin}\left(\mathrm{8x}\right)\mathrm{cos}\left(\mathrm{2x}\right)−\mathrm{sin}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{8x}\right)\right]−\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{sin}\left(\mathrm{8x}\right)\mathrm{cos}\left(\mathrm{x}\right)+\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{8x}\right)−\left[\mathrm{sin}\left(\mathrm{8x}\right)\mathrm{cos}\left(\mathrm{x}\right)−\mathrm{sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{8x}\right)\right]−\mathrm{sin}\left(\mathrm{x}\right)} \\ $$$$=\frac{\mathrm{2sin}\left(\mathrm{2x}\right)\mathrm{cos}\left(\mathrm{8x}\right)−\mathrm{sin}\left(\mathrm{2x}\right)}{\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{8x}\right)−\mathrm{sin}\left(\mathrm{x}\right)}=\frac{\mathrm{sin}\left(\mathrm{2x}\right)\left[\mathrm{2cos}\left(\mathrm{8x}\right)−\mathrm{1}\right]}{\mathrm{sin}\left(\mathrm{x}\right)\left[\mathrm{2cos}\left(\mathrm{8x}\right)−\mathrm{1}\right]}=\frac{\mathrm{2sin}\left(\mathrm{x}\right)\mathrm{cos}\left(\mathrm{x}\right)}{\mathrm{sin}\left(\mathrm{x}\right)} \\ $$$$\mathrm{I}=\mathrm{2cos}\left(\mathrm{x}\right) \\ $$
