Menu Close

Test-for-convergence-1-n-10-2-ln-lnn-nlnn-2-n-2-1-n-lnn-p-two-cases-of-p-to-look-at-3-n-2-1-n-n-lnn-4-n-1-10-n-n-2n-1-5-n-1-

Tinku Tara 0 Comments
Pin




Question Number 3564 by Yozzii last updated on 15/Dec/15
Test for convergence: (1) Σ_(n=10) ^∞ (2^(ln(lnn)) /(nlnn)) (2)Σ_(n=2) ^∞ (1/(n(lnn)^p )) (two cases of p to look at) (3)Σ_(n=2) ^∞ (((−1)^n (√n))/(lnn)) (4)Σ_(n=1) ^∞ ((10^n n)/((2n+1)!)) (5)Σ_(n=1) ^∞ ((n!)/n^n ) This post is my attempt to adhere to the common agreement on infinite series studying. Have fun!
$${Test}\:{for}\:{convergence}: \\ $$$$\left(\mathrm{1}\right)\:\underset{{n}=\mathrm{10}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{\mathrm{ln}\left(\mathrm{ln}{n}\right)} }{{n}\mathrm{ln}{n}} \\ $$$$\left(\mathrm{2}\right)\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left(\mathrm{ln}{n}\right)^{\mathrm{p}} }\:\left(\mathrm{two}\:\mathrm{cases}\:\mathrm{of}\:\mathrm{p}\:\mathrm{to}\:\mathrm{look}\:\mathrm{at}\right) \\ $$$$\left(\mathrm{3}\right)\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} \sqrt{{n}}}{\mathrm{ln}{n}} \\ $$$$\left(\mathrm{4}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{10}^{{n}} {n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!} \\ $$$$\left(\mathrm{5}\right)\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}!}{{n}^{{n}} } \\ $$$${This}\:{post}\:{is}\:{my}\:{attempt}\:{to}\:{adhere}\:{to} \\ $$$${the}\:{common}\:{agreement}\:{on}\:{infinite} \\ $$$${series}\:{studying}.\:{Have}\:{fun}! \\ $$
Commented by prakash jain last updated on 15/Dec/15
Find sum or only check for convergence?
$$\mathrm{Find}\:\mathrm{sum}\:\mathrm{or}\:\mathrm{only}\:\mathrm{check}\:\mathrm{for}\:\mathrm{convergence}? \\ $$
Commented by Yozzii last updated on 15/Dec/15
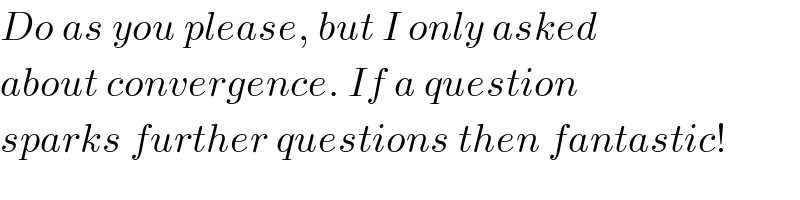
Do as you please, but I only asked about convergence. If a question sparks further questions then fantastic!
$${Do}\:{as}\:{you}\:{please},\:{but}\:{I}\:{only}\:{asked}\: \\ $$$${about}\:{convergence}.\:{If}\:{a}\:{question} \\ $$$${sparks}\:{further}\:{questions}\:{then}\:{fantastic}! \\ $$
Answered by prakash jain last updated on 15/Dec/15
5. a_n =((n!)/n^n ), a_(n+1) =(((n+1)!)/((n+1)^(n+1) )) (a_(n+1) /a_n )=(((n+1)!n^n )/(n!(n+1)^(n+1) ))=(((n+1)n^n )/((n+1)(n+1)^n ))=((n/(1+n)))^n lim_(n→∞) ((n/(1+n)))^n =lim_(x→0) (((1/x)/(1+1/x)))^(1/x) =lim_(x→0) ((1/(1+x)))^(1/x) y=((1/(1+x)))^(1/x) ⇒ln y=−((ln (1+x))/x) lim_(x→0) ln y=lim_(x→0) −((1/(1+x))/1)=−1 lim_(x→0) ((1/(1+x)))^(1/x) =(1/e) (1/e)<1, hence by ratio test series converges.
$$\mathrm{5}.\:{a}_{{n}} =\frac{{n}!}{{n}^{{n}} },\:{a}_{{n}+\mathrm{1}} =\frac{\left({n}+\mathrm{1}\right)!}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} } \\ $$$$\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }=\frac{\left({n}+\mathrm{1}\right)!{n}^{{n}} }{{n}!\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }=\frac{\left({n}+\mathrm{1}\right){n}^{{n}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{1}\right)^{{n}} }=\left(\frac{{n}}{\mathrm{1}+{n}}\right)^{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{{n}}{\mathrm{1}+{n}}\right)^{{n}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}/{x}}{\mathrm{1}+\mathrm{1}/{x}}\right)^{\mathrm{1}/{x}} =\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)^{\mathrm{1}/{x}} \\ $$$${y}=\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)^{\mathrm{1}/{x}} \Rightarrow\mathrm{ln}\:{y}=−\frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\right)}{{x}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{ln}\:{y}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\frac{\mathrm{1}}{\mathrm{1}+{x}}}{\mathrm{1}}=−\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\right)^{\mathrm{1}/{x}} =\frac{\mathrm{1}}{{e}} \\ $$$$\frac{\mathrm{1}}{{e}}<\mathrm{1},\:\mathrm{hence}\:\mathrm{by}\:\mathrm{ratio}\:\mathrm{test}\:\mathrm{series}\:\mathrm{converges}. \\ $$
Answered by prakash jain last updated on 15/Dec/15
4. a_n =((10^n n)/((2n+1)!)) ⇒ (a_(n+1) /a_n )=((10(n+1))/(n(2n+2)(2n+3))) lim_(n→∞) ((10(n+1))/(n(2n+2)(2n+3)))=0 series converges
$$\mathrm{4}.\:{a}_{{n}} =\frac{\mathrm{10}^{{n}} {n}}{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\Rightarrow\:\:\frac{{a}_{{n}+\mathrm{1}} }{{a}_{{n}} }=\frac{\mathrm{10}\left({n}+\mathrm{1}\right)}{{n}\left(\mathrm{2}{n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{10}\left({n}+\mathrm{1}\right)}{{n}\left(\mathrm{2}{n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}=\mathrm{0} \\ $$$$\mathrm{series}\:\mathrm{converges} \\ $$
Answered by prakash jain last updated on 15/Dec/15
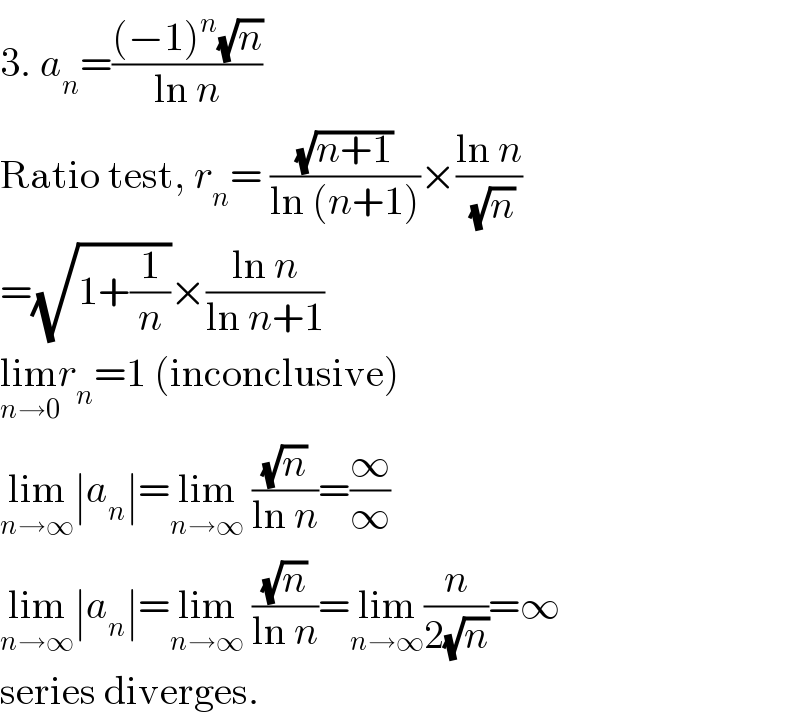
3. a_n =(((−1)^n (√n))/(ln n)) Ratio test, r_n = ((√(n+1))/(ln (n+1)))×((ln n)/( (√n))) =(√(1+(1/n)))×((ln n)/(ln n+1)) lim_(n→0) r_n =1 (inconclusive) lim_(n→∞) ∣a_n ∣=lim_(n→∞) ((√n)/(ln n))=(∞/∞) lim_(n→∞) ∣a_n ∣=lim_(n→∞) ((√n)/(ln n))=lim_(n→∞) (n/(2(√n)))=∞ series diverges.
$$\mathrm{3}.\:{a}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}} \sqrt{{n}}}{\mathrm{ln}\:{n}} \\ $$$$\mathrm{Ratio}\:\mathrm{test},\:{r}_{{n}} =\:\frac{\sqrt{{n}+\mathrm{1}}}{\mathrm{ln}\:\left({n}+\mathrm{1}\right)}×\frac{\mathrm{ln}\:{n}}{\:\sqrt{{n}}} \\ $$$$=\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}}}×\frac{\mathrm{ln}\:{n}}{\mathrm{ln}\:{n}+\mathrm{1}} \\ $$$$\underset{{n}\rightarrow\mathrm{0}} {\mathrm{lim}}{r}_{{n}} =\mathrm{1}\:\left(\mathrm{inconclusive}\right) \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\mid{a}_{{n}} \mid=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{{n}}}{\mathrm{ln}\:{n}}=\frac{\infty}{\infty} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\mid{a}_{{n}} \mid=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\sqrt{{n}}}{\mathrm{ln}\:{n}}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{{n}}{\mathrm{2}\sqrt{{n}}}=\infty \\ $$$$\mathrm{series}\:\mathrm{diverges}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *