Question Number 66010 by jimful last updated on 07/Aug/19
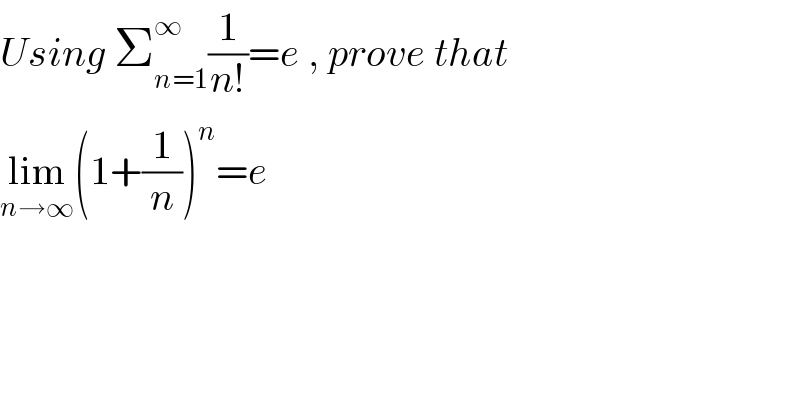
$${Using}\:\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{{n}!}={e}\:,\:{prove}\:{that} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} ={e} \\ $$
Commented by Prithwish sen last updated on 07/Aug/19

$$=\mathrm{1}+\mathrm{n}.\frac{\mathrm{1}}{\mathrm{n}}+\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\frac{\mathrm{1}}{\mathrm{2}.\mathrm{n}^{\:\mathrm{2}} }\:+\mathrm{n}\left(\mathrm{m}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\frac{\mathrm{1}}{\mathrm{3}!\mathrm{n}^{\mathrm{3}} }+…. \\ $$$$=\mathrm{1}+\mathrm{1}+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}\right)\frac{\mathrm{1}}{\mathrm{2}!}+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}}\right)\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{n}}\right)\frac{\mathrm{1}}{\mathrm{3}!}+… \\ $$$$=\mathrm{1}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{1}}{\mathrm{3}!}+….\:\:\mathrm{as}\:\mathrm{n}\rightarrow\infty\:\Rightarrow\frac{\mathrm{1}}{\mathrm{n}}\:\rightarrow\:\mathrm{0} \\ $$$$=\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{n}!}\:=\:\mathrm{e}\:\:\mathrm{please}\:\mathrm{check}. \\ $$
