What-will-be-the-minimum-area-of-a-heptagon-inscribed-in-an-unit-square-

Question Number 134002 by Dwaipayan Shikari last updated on 26/Feb/21

W h a t w i l l b e t h e m i n i m u m a r e a o f a h e p t a g o n i n s c r i b e d i n

a n u n i t s q u a r e ?

Commented by Dwaipayan Shikari last updated on 26/Feb/21

Answered by mr W last updated on 26/Feb/21

Commented by mr W last updated on 26/Feb/21

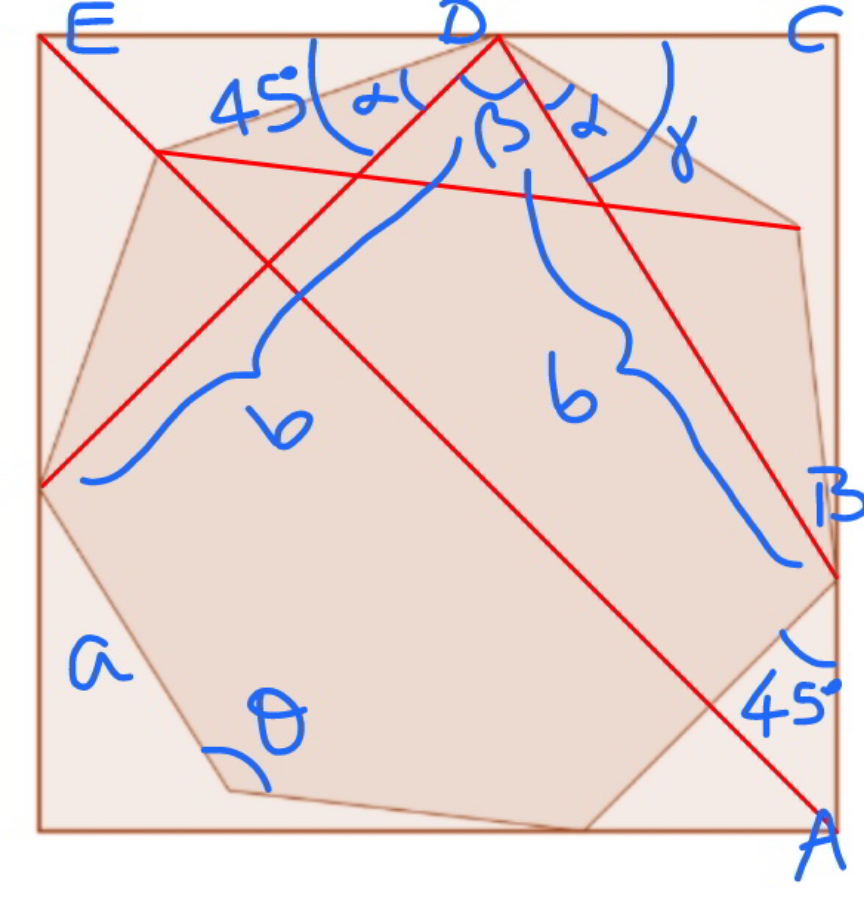
s i d e l e n g t h o f h e p t a g o n = a

θ = \frac{(7 - 2) \times 180 °}{7} = \frac{900 °}{7}

α = 90 ° - \frac{θ}{2} = \frac{180 °}{7}

β = θ - 2 α = \frac{540 °}{7}

γ = 180 ° - 45 ° - β = \frac{405 °}{7}

D B = b = 2 a \cos α = 2 a \cos \frac{180 °}{7}

A B = \frac{a}{\sqrt{2}}

B C = b \sin γ = 2 a \cos \frac{180 °}{7} \sin \frac{405 °}{7}

A C = (\frac{1}{\sqrt{2}} + 2 \cos \frac{180 °}{7} \sin \frac{405 °}{7}) a = 1

\Rightarrow a = \frac{1}{\frac{1}{\sqrt{2}} + 2 \cos \frac{180 °}{7} \sin \frac{405 °}{7}}

a r e a o f h e p t a g o n

A = \frac{7 a^{2}}{4 \tan \frac{180 °}{7}}

= \frac{7}{4 \tan \frac{180 °}{7} {(\frac{1}{\sqrt{2}} + 2 \cos \frac{180 °}{7} \sin \frac{405 °}{7})}^{2}}

\approx 0.728 878 175

c h e c k :

E D = \frac{b}{\sqrt{2}}

D C = b \cos γ

E C = b (\frac{1}{\sqrt{2}} + \cos γ) = 2 a \cos \frac{180 °}{7} (\frac{1}{\sqrt{2}} + \cos \frac{405 °}{7})

= 2 \times \frac{1}{\frac{1}{\sqrt{2}} + 2 \cos \frac{180 °}{7} \sin \frac{405 °}{7}} \times \cos \frac{180 °}{7} (\frac{1}{\sqrt{2}} + \cos \frac{405 °}{7})

= 1

Commented by Dwaipayan Shikari last updated on 26/Feb/21

G r e a t s i r!