Question Number 776 by 123456 last updated on 12/Mar/15
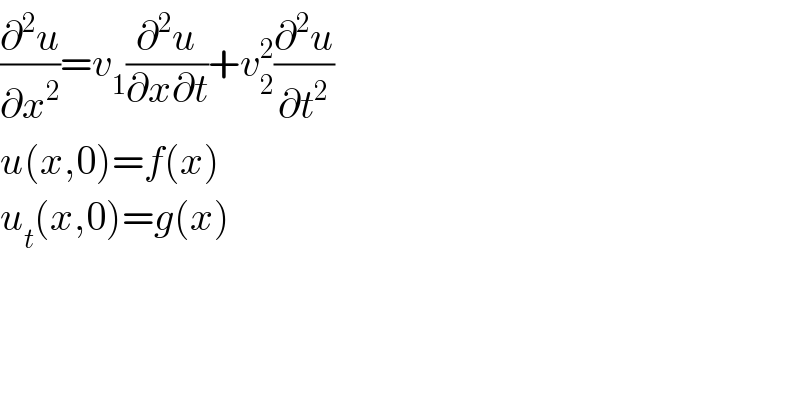
$$\frac{\partial^{\mathrm{2}} {u}}{\partial{x}^{\mathrm{2}} }={v}_{\mathrm{1}} \frac{\partial^{\mathrm{2}} {u}}{\partial{x}\partial{t}}+{v}_{\mathrm{2}} ^{\mathrm{2}} \frac{\partial^{\mathrm{2}} {u}}{\partial{t}^{\mathrm{2}} } \\ $$$${u}\left({x},\mathrm{0}\right)={f}\left({x}\right) \\ $$$${u}_{{t}} \left({x},\mathrm{0}\right)={g}\left({x}\right) \\ $$
Commented by prakash jain last updated on 12/Mar/15
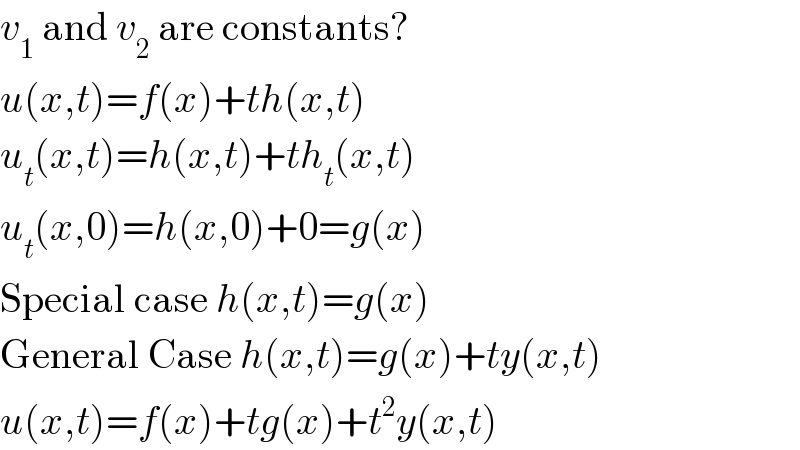
$${v}_{\mathrm{1}} \:\mathrm{and}\:{v}_{\mathrm{2}} \:\mathrm{are}\:\mathrm{constants}? \\ $$$${u}\left({x},{t}\right)={f}\left({x}\right)+{th}\left({x},{t}\right) \\ $$$${u}_{{t}} \left({x},{t}\right)={h}\left({x},{t}\right)+{th}_{{t}} \left({x},{t}\right) \\ $$$${u}_{{t}} \left({x},\mathrm{0}\right)={h}\left({x},\mathrm{0}\right)+\mathrm{0}={g}\left({x}\right) \\ $$$$\mathrm{Special}\:\mathrm{case}\:{h}\left({x},{t}\right)={g}\left({x}\right) \\ $$$$\mathrm{General}\:\mathrm{Case}\:{h}\left({x},{t}\right)={g}\left({x}\right)+{ty}\left({x},{t}\right) \\ $$$${u}\left({x},{t}\right)={f}\left({x}\right)+{tg}\left({x}\right)+{t}^{\mathrm{2}} {y}\left({x},{t}\right) \\ $$
Commented by prakash jain last updated on 12/Mar/15
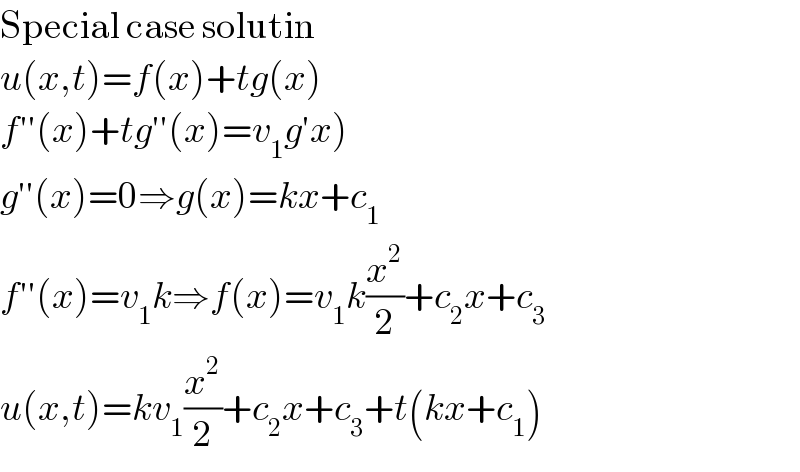
$$\mathrm{Special}\:\mathrm{case}\:\mathrm{solutin} \\ $$$${u}\left({x},{t}\right)={f}\left({x}\right)+{tg}\left({x}\right) \\ $$$$\left.{f}''\left({x}\right)+{tg}''\left({x}\right)={v}_{\mathrm{1}} {g}'{x}\right) \\ $$$${g}''\left({x}\right)=\mathrm{0}\Rightarrow{g}\left({x}\right)={kx}+{c}_{\mathrm{1}} \\ $$$${f}''\left({x}\right)={v}_{\mathrm{1}} {k}\Rightarrow{f}\left({x}\right)={v}_{\mathrm{1}} {k}\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{c}_{\mathrm{2}} {x}+{c}_{\mathrm{3}} \\ $$$${u}\left({x},{t}\right)={kv}_{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{c}_{\mathrm{2}} {x}+{c}_{\mathrm{3}} +{t}\left({kx}+{c}_{\mathrm{1}} \right) \\ $$
Answered by prakash jain last updated on 12/Mar/15
![u(x,t)=f(x)+tg(x)+t^2 y(x,t) (∂u/∂t)=2ty+t^2 (∂y/∂t)+g(x) (∂^2 u/∂t^2 )=2t(∂y/∂t)+2y+t^2 (∂^2 y/∂t^2 )+2t(∂y/∂t)=2y+4t(∂y/∂t)+t^2 (∂^2 y/∂t^2 ) f′′(x)+tg′′(x)+t^2 (∂^2 y/∂x^2 ) =v_1 [2t(∂y/∂x)+g′(x)+t^2 (∂^2 y/(∂x∂t))]+v_2 ^2 [2y+4t(∂y/∂t)+t^2 (∂^2 y/∂t^2 )] This needs to be solved for general case.](https://www.tinkutara.com/question/Q780.png)
$${u}\left({x},{t}\right)={f}\left({x}\right)+{tg}\left({x}\right)+{t}^{\mathrm{2}} {y}\left({x},{t}\right) \\ $$$$\frac{\partial{u}}{\partial{t}}=\mathrm{2}{ty}+{t}^{\mathrm{2}} \frac{\partial{y}}{\partial{t}}+{g}\left({x}\right) \\ $$$$\frac{\partial^{\mathrm{2}} {u}}{\partial{t}^{\mathrm{2}} }=\mathrm{2}{t}\frac{\partial{y}}{\partial{t}}+\mathrm{2}{y}+{t}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} {y}}{\partial{t}^{\mathrm{2}} }+\mathrm{2}{t}\frac{\partial{y}}{\partial{t}}=\mathrm{2}{y}+\mathrm{4}{t}\frac{\partial{y}}{\partial{t}}+{t}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} {y}}{\partial{t}^{\mathrm{2}} } \\ $$$${f}''\left({x}\right)+{tg}''\left({x}\right)+{t}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} {y}}{\partial{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:={v}_{\mathrm{1}} \left[\mathrm{2}{t}\frac{\partial{y}}{\partial{x}}+{g}'\left({x}\right)+{t}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} {y}}{\partial{x}\partial{t}}\right]+{v}_{\mathrm{2}} ^{\mathrm{2}} \left[\mathrm{2}{y}+\mathrm{4}{t}\frac{\partial{y}}{\partial{t}}+{t}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} {y}}{\partial{t}^{\mathrm{2}} }\right] \\ $$$$\mathrm{This}\:\mathrm{needs}\:\mathrm{to}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{for}\:\mathrm{general}\:\mathrm{case}. \\ $$
Commented by prakash jain last updated on 12/Mar/15
![Try y=C g(x)=kx+c_1 f′′(x)=kv_1 +2Cv_2 ^2 f(x)=(x^2 /2)[kv_1 +2Cv_2 ^2 ]+c_2 x+c_3 u(x,t)=f(x)+tg(x)+Ct^2 (∂^2 u/∂t^2 )=2C (∂u/∂t)=g(x)+2Ct (∂^2 u/(∂x∂t))=k (∂^2 u/∂x^2 )=kv_1 +2Cv_2 ^2 The solution meets all given conditions. So given any y(x,t) a solution for u(x,t) can be found.](https://www.tinkutara.com/question/Q782.png)
$$\mathrm{Try}\:{y}={C} \\ $$$${g}\left({x}\right)={kx}+{c}_{\mathrm{1}} \\ $$$${f}''\left({x}\right)={kv}_{\mathrm{1}} +\mathrm{2}{Cv}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${f}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left[{kv}_{\mathrm{1}} +\mathrm{2}{Cv}_{\mathrm{2}} ^{\mathrm{2}} \right]+{c}_{\mathrm{2}} {x}+{c}_{\mathrm{3}} \\ $$$${u}\left({x},{t}\right)={f}\left({x}\right)+{tg}\left({x}\right)+{Ct}^{\mathrm{2}} \\ $$$$\frac{\partial^{\mathrm{2}} {u}}{\partial{t}^{\mathrm{2}} }=\mathrm{2}{C} \\ $$$$\frac{\partial{u}}{\partial{t}}={g}\left({x}\right)+\mathrm{2}{Ct} \\ $$$$\frac{\partial^{\mathrm{2}} {u}}{\partial{x}\partial{t}}={k} \\ $$$$\frac{\partial^{\mathrm{2}} {u}}{\partial{x}^{\mathrm{2}} }={kv}_{\mathrm{1}} +\mathrm{2}{Cv}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$$\mathrm{The}\:\mathrm{solution}\:\mathrm{meets}\:\mathrm{all}\:\mathrm{given}\:\mathrm{conditions}. \\ $$$$\mathrm{So}\:\mathrm{given}\:\mathrm{any}\:{y}\left({x},{t}\right)\:\mathrm{a}\:\mathrm{solution}\:\mathrm{for}\:{u}\left({x},{t}\right) \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{found}. \\ $$
