Question Number 131849 by mnjuly1970 last updated on 09/Feb/21

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\ast\ast\ast\:\:\:{calculus}\:\left({I}\right)\:\ast\ast\ast \\ $$$$\:\:\:{please}\:\:{evaluate}:: \\ $$$$\:\:\:\:\:\:\:\:\phi=\int\frac{{dx}}{{sin}\left(\mathrm{2}{x}\right){ln}\left({tan}\left({x}\right)\right)} \\ $$$$\:\:\:\:\:\:{Trinity}\:{College} \\ $$$$\:\:\:\:\:\:\:{Cambridge}\:….\mathrm{1897}… \\ $$
Answered by mindispower last updated on 09/Feb/21
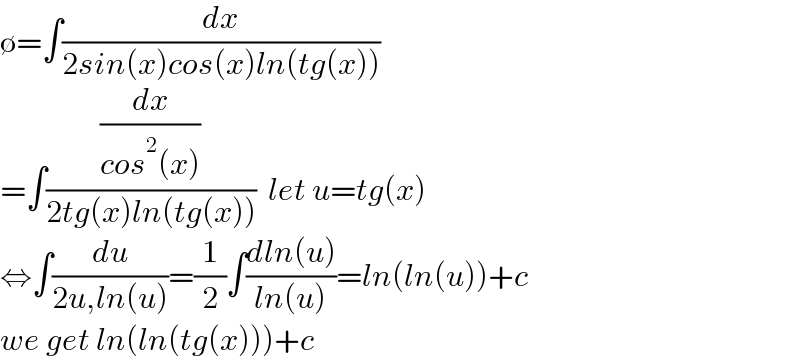
$$\emptyset=\int\frac{{dx}}{\mathrm{2}{sin}\left({x}\right){cos}\left({x}\right){ln}\left({tg}\left({x}\right)\right)} \\ $$$$=\int\frac{\frac{{dx}}{{cos}^{\mathrm{2}} \left({x}\right)}}{\mathrm{2}{tg}\left({x}\right){ln}\left({tg}\left({x}\right)\right)}\:\:{let}\:{u}={tg}\left({x}\right) \\ $$$$\Leftrightarrow\int\frac{{du}}{\mathrm{2}{u},{ln}\left({u}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dln}\left({u}\right)}{{ln}\left({u}\right)}={ln}\left({ln}\left({u}\right)\right)+{c} \\ $$$${we}\:{get}\:{ln}\left({ln}\left({tg}\left({x}\right)\right)\right)+{c} \\ $$
Commented by mnjuly1970 last updated on 09/Feb/21
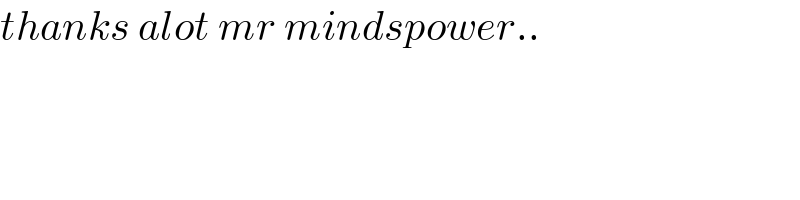
$${thanks}\:{alot}\:{mr}\:{mindspower}.. \\ $$
Answered by Dwaipayan Shikari last updated on 09/Feb/21
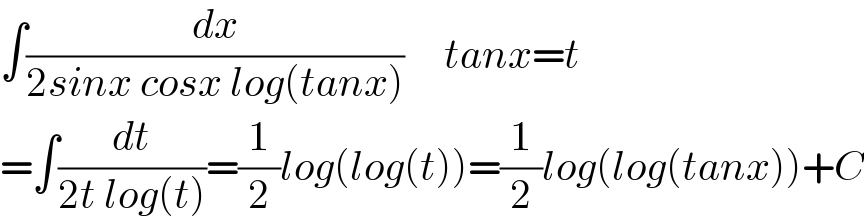
$$\int\frac{{dx}}{\mathrm{2}{sinx}\:{cosx}\:{log}\left({tanx}\right)}\:\:\:\:\:{tanx}={t} \\ $$$$=\int\frac{{dt}}{\mathrm{2}{t}\:{log}\left({t}\right)}=\frac{\mathrm{1}}{\mathrm{2}}{log}\left({log}\left({t}\right)\right)=\frac{\mathrm{1}}{\mathrm{2}}{log}\left({log}\left({tanx}\right)\right)+{C} \\ $$
Commented by mnjuly1970 last updated on 09/Feb/21

$${mercey}\:\:{mr}\:{dwaipayan}… \\ $$
Answered by mnjuly1970 last updated on 09/Feb/21
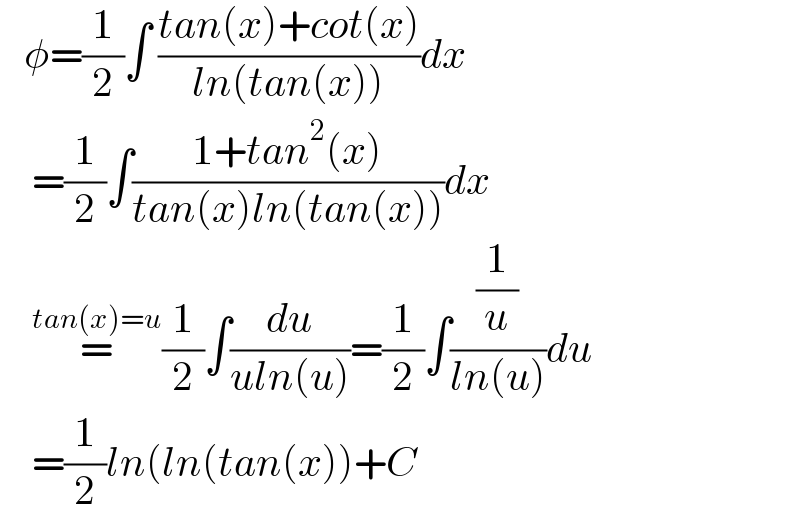
$$\:\:\:\phi=\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{tan}\left({x}\right)+{cot}\left({x}\right)}{{ln}\left({tan}\left({x}\right)\right)}{dx} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}+{tan}^{\mathrm{2}} \left({x}\right)}{{tan}\left({x}\right){ln}\left({tan}\left({x}\right)\right)}{dx} \\ $$$$\:\:\:\:\overset{{tan}\left({x}\right)={u}} {=}\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{{uln}\left({u}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\frac{\mathrm{1}}{{u}}}{{ln}\left({u}\right)}{du} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({ln}\left({tan}\left({x}\right)\right)+{C}\right. \\ $$
