Question Number 3546 by prakash jain last updated on 15/Dec/15

$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{p}_{{i}} },\:{p}_{{i}} \:{is}\:{i}^{{th}} \:{prime}\:{diverges}. \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{s}_{{i}} },\:{s}_{{i}} \:{is}\:{i}^{{th}} \:{whole}\:{square}\:{converges}. \\ $$$$\mathrm{Why}? \\ $$$$\mathrm{Even}\:\mathrm{though}\:\mathrm{it}\:\mathrm{appears}\:\mathrm{that}\:\mathrm{we}\:\mathrm{have}\:\mathrm{more} \\ $$$$\mathrm{whole}\:\mathrm{squares}\:\mathrm{than}\:\mathrm{primes}. \\ $$
Commented by Yozzii last updated on 15/Dec/15

$${Yes}. \\ $$
Commented by prakash jain last updated on 15/Dec/15

$$\mathrm{Thanks}.\:\mathrm{It}\:\mathrm{answers}\:\mathrm{the}\:\mathrm{question}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{inverse}\:\mathrm{of}\:\mathrm{prime}\:\mathrm{number}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{divergent}\:\mathrm{if}\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\mathrm{is}\:\mathrm{convergent}. \\ $$
Commented by Filup last updated on 15/Dec/15
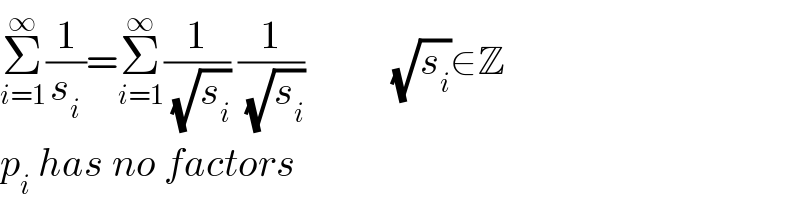
$$\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{s}_{{i}} }=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{s}_{{i}} }}\:\frac{\mathrm{1}}{\:\sqrt{{s}_{{i}} }}\:\:\:\:\:\:\:\:\:\:\:\sqrt{{s}_{{i}} }\in\mathbb{Z} \\ $$$${p}_{{i}} \:{has}\:{no}\:{factors} \\ $$
Commented by Yozzii last updated on 15/Dec/15
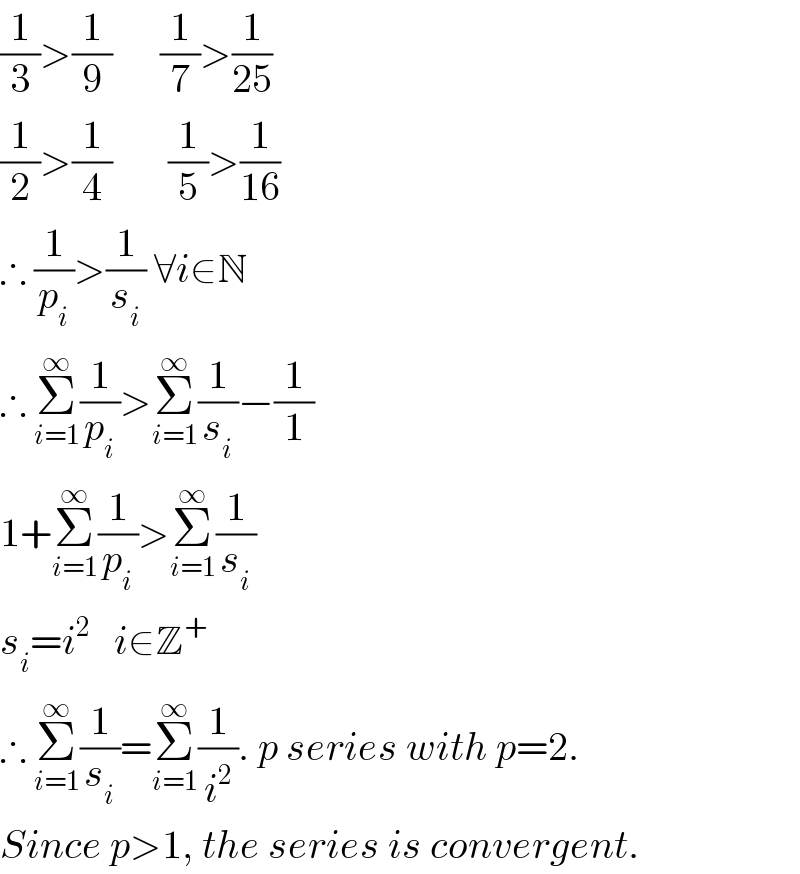
$$\frac{\mathrm{1}}{\mathrm{3}}>\frac{\mathrm{1}}{\mathrm{9}}\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{7}}>\frac{\mathrm{1}}{\mathrm{25}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}>\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{5}}>\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\therefore\:\frac{\mathrm{1}}{{p}_{{i}} }>\frac{\mathrm{1}}{{s}_{{i}} }\:\forall{i}\in\mathbb{N} \\ $$$$\therefore\:\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{p}_{{i}} }>\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{s}_{{i}} }−\frac{\mathrm{1}}{\mathrm{1}} \\ $$$$\mathrm{1}+\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{p}_{{i}} }>\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{s}_{{i}} } \\ $$$${s}_{{i}} ={i}^{\mathrm{2}} \:\:\:{i}\in\mathbb{Z}^{+} \: \\ $$$$\therefore\:\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{s}_{{i}} }=\underset{{i}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{i}^{\mathrm{2}} }.\:{p}\:{series}\:{with}\:{p}=\mathrm{2}. \\ $$$${Since}\:{p}>\mathrm{1},\:{the}\:{series}\:{is}\:{convergent}. \\ $$
