Menu Close

If-F-y-f-z-z-f-y-i-z-f-x-x-f-z-j-x-f-y-y-f-x-k-prove-that-F-r-f-

Tinku Tara
Pin




Question Number 4 by user1 last updated on 25/Jan/15
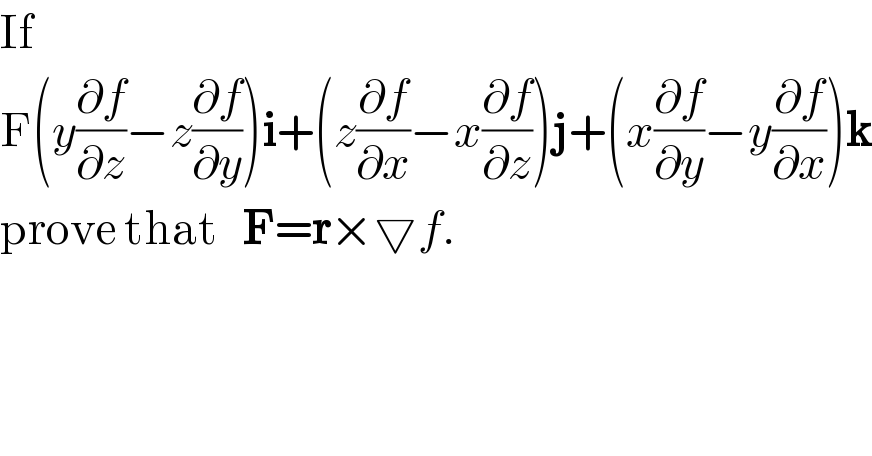
If F(y(∂f/∂z)−z(∂f/∂y))i+(z(∂f/∂x)−x(∂f/∂z))j+(x(∂f/∂y)−y(∂f/∂x))k prove that F=r×▽f.
$$\mathrm{If} \\ $$$$\mathrm{F}\left({y}\frac{\partial{f}}{\partial{z}}−{z}\frac{\partial{f}}{\partial{y}}\right)\boldsymbol{\mathrm{i}}+\left({z}\frac{\partial{f}}{\partial{x}}−{x}\frac{\partial{f}}{\partial{z}}\right)\boldsymbol{\mathrm{j}}+\left({x}\frac{\partial{f}}{\partial{y}}−{y}\frac{\partial{f}}{\partial{x}}\right)\boldsymbol{\mathrm{k}} \\ $$$$\mathrm{prove}\:\mathrm{that}\:\:\:\boldsymbol{\mathrm{F}}=\boldsymbol{\mathrm{r}}×\bigtriangledown{f}. \\ $$
Answered by user1 last updated on 29/Oct/14
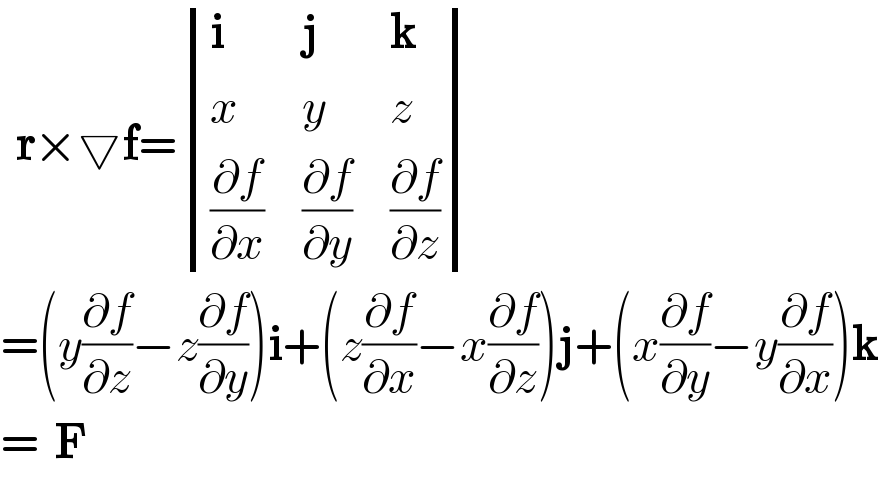
r×▽f= determinant ((i,j,k),(x,y,z),((∂f/∂x),(∂f/∂y),(∂f/∂z))) =(y(∂f/∂z)−z(∂f/∂y))i+(z(∂f/∂x)−x(∂f/∂z))j+(x(∂f/∂y)−y(∂f/∂x))k = F
$$\:\:\boldsymbol{\mathrm{r}}×\bigtriangledown\boldsymbol{\mathrm{f}}=\begin{vmatrix}{\boldsymbol{\mathrm{i}}}&{\boldsymbol{\mathrm{j}}}&{\boldsymbol{\mathrm{k}}}\\{{x}}&{{y}}&{{z}}\\{\frac{\partial{f}}{\partial{x}}}&{\frac{\partial{f}}{\partial{y}}}&{\frac{\partial{f}}{\partial{z}}}\end{vmatrix} \\ $$$$=\left({y}\frac{\partial{f}}{\partial{z}}−{z}\frac{\partial{f}}{\partial{y}}\right)\boldsymbol{\mathrm{i}}+\left({z}\frac{\partial{f}}{\partial{x}}−{x}\frac{\partial{f}}{\partial{z}}\right)\boldsymbol{\mathrm{j}}+\left({x}\frac{\partial{f}}{\partial{y}}−{y}\frac{\partial{f}}{\partial{x}}\right)\boldsymbol{\mathrm{k}} \\ $$$$=\:\:\boldsymbol{\mathrm{F}} \\ $$

Pin