Is-there-a-solution-to-i-a-n-i-i-a-n-i-n-a-Z-

Question Number 3193 by Filup last updated on 07/Dec/15

Is there a solution to: Σ_(i=a) ^n i=Π_(i=a) ^n i (n, a)∈Z

$$\mathrm{Is}\:\mathrm{there}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{to}: \\ $$$$\underset{{i}={a}} {\overset{{n}} {\sum}}{i}=\underset{{i}={a}} {\overset{{n}} {\prod}}{i}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({n},\:{a}\right)\in\mathbb{Z} \\ $$

Commented by Filup last updated on 07/Dec/15

Σ_(i=a) ^n i=(1/2)n(a+n) Π_(i=a) ^n i=((n!)/((a−1)!)) ∴(1/2)n(a+n)=((n!)/((a−1)!))

$$\underset{{i}={a}} {\overset{{n}} {\sum}}{i}=\frac{\mathrm{1}}{\mathrm{2}}{n}\left({a}+{n}\right) \\ $$$$\underset{{i}={a}} {\overset{{n}} {\prod}}{i}=\frac{{n}!}{\left({a}−\mathrm{1}\right)!} \\ $$$$ \\ $$$$\therefore\frac{\mathrm{1}}{\mathrm{2}}{n}\left({a}+{n}\right)=\frac{{n}!}{\left({a}−\mathrm{1}\right)!} \\ $$

Commented by prakash jain last updated on 07/Dec/15

n=a n=a Π_(i=a) ^n i=a=Σ_(i=a) ^n i your formula for Σ_(i=a) ^n i is incorrect. it should be=((n−a+1)/2)(a+n) If n>a and a>1 a(a+1)≠a+a+1 so no solutions for n>a n<a LHS=0=RHS

$${n}={a}\: \\ $$$${n}={a}\:\underset{{i}={a}} {\overset{{n}} {\prod}}{i}={a}=\underset{{i}={a}} {\overset{{n}} {\sum}}{i} \\ $$$${your}\:{formula}\:{for}\:\underset{{i}={a}} {\overset{{n}} {\sum}}{i}\:\mathrm{is}\:\mathrm{incorrect}.\:\mathrm{it}\:\mathrm{should} \\ $$$$\mathrm{be}=\frac{{n}−{a}+\mathrm{1}}{\mathrm{2}}\left({a}+{n}\right) \\ $$$$\mathrm{If}\:{n}>{a}\:{and}\:{a}>\mathrm{1} \\ $$$${a}\left({a}+\mathrm{1}\right)\neq{a}+{a}+\mathrm{1} \\ $$$${so}\:{no}\:{solutions}\:{for}\:{n}>{a} \\ $$$${n}<{a}\:\mathrm{LHS}=\mathrm{0}=\mathrm{RHS} \\ $$

Commented by Filup last updated on 07/Dec/15

Thanks for the correction! What if a,n∈R? Same result?

$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{the}\:\mathrm{correction}! \\ $$$$\mathrm{W}{hat}\:\mathrm{if}\:\:\:\:\:{a},{n}\in\mathbb{R}? \\ $$$${Same}\:{result}? \\ $$

Commented by Filup last updated on 07/Dec/15

What if a+(a+1)+...+(n)=a(a+1)...n for (a, n)∈R

$$\mathrm{What}\:\mathrm{if} \\ $$$${a}+\left({a}+\mathrm{1}\right)+…+\left({n}\right)={a}\left({a}+\mathrm{1}\right)…{n} \\ $$$${for}\:\:\left({a},\:{n}\right)\in\mathbb{R} \\ $$

Commented by prakash jain last updated on 07/Dec/15

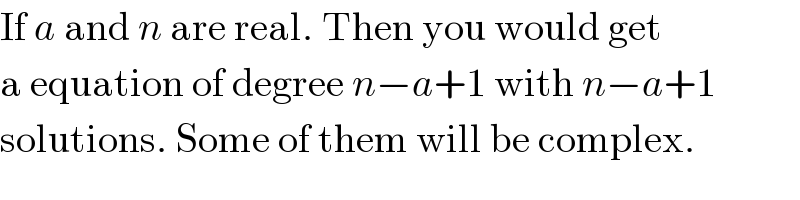
If a and n are real. Then you would get a equation of degree n−a+1 with n−a+1 solutions. Some of them will be complex.

$$\mathrm{If}\:{a}\:\mathrm{and}\:{n}\:\mathrm{are}\:\mathrm{real}.\:\mathrm{Then}\:\mathrm{you}\:\mathrm{would}\:\mathrm{get} \\ $$$$\mathrm{a}\:\mathrm{equation}\:\mathrm{of}\:\mathrm{degree}\:{n}−{a}+\mathrm{1}\:\mathrm{with}\:{n}−{a}+\mathrm{1} \\ $$$$\mathrm{solutions}.\:\mathrm{Some}\:\mathrm{of}\:\mathrm{them}\:\mathrm{will}\:\mathrm{be}\:\mathrm{complex}. \\ $$

Facebook Tweet Pin

Is-there-a-solution-to-i-a-n-i-i-a-n-i-n-a-Z-

Leave a Reply Cancel reply