Menu Close

let-S-a-1-a-2-a-n-S-n-S-contains-n-random-integers-such-that-a-a-k-b-If-I-wanted-to-find-the-average-value-which-is-S-1-n-i-1-n-a-i-What-would-a-possible-answer-be-

Tinku Tara 0 Comments
Pin




Question Number 3112 by Filup last updated on 05/Dec/15
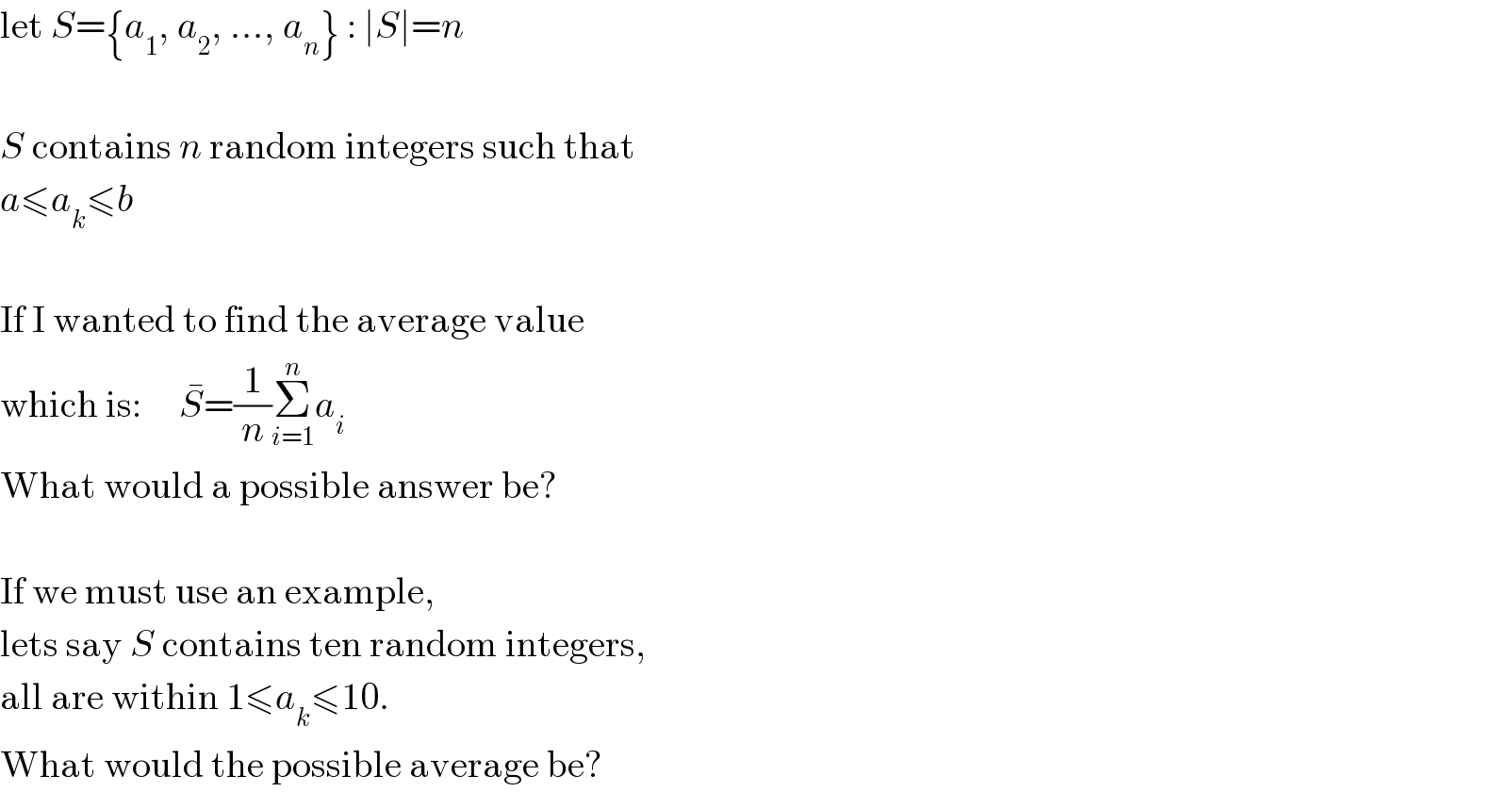
let S={a_1 , a_2 , ..., a_n } : ∣S∣=n S contains n random integers such that a≤a_k ≤b If I wanted to find the average value which is: S^� =(1/n)Σ_(i=1) ^n a_i What would a possible answer be? If we must use an example, lets say S contains ten random integers, all are within 1≤a_k ≤10. What would the possible average be?
$$\mathrm{let}\:{S}=\left\{{a}_{\mathrm{1}} ,\:{a}_{\mathrm{2}} ,\:…,\:{a}_{{n}} \right\}\::\:\mid{S}\mid={n} \\ $$$$ \\ $$$${S}\:\mathrm{contains}\:{n}\:\mathrm{random}\:\mathrm{integers}\:\mathrm{such}\:\mathrm{that} \\ $$$${a}\leqslant{a}_{{k}} \leqslant{b} \\ $$$$ \\ $$$$\mathrm{If}\:\mathrm{I}\:\mathrm{wanted}\:\mathrm{to}\:\mathrm{find}\:\mathrm{the}\:\mathrm{average}\:\mathrm{value} \\ $$$$\mathrm{which}\:\mathrm{is}:\:\:\:\:\:\bar {{S}}=\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} \\ $$$$\mathrm{What}\:\mathrm{would}\:\mathrm{a}\:\mathrm{possible}\:\mathrm{answer}\:\mathrm{be}? \\ $$$$ \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{must}\:\mathrm{use}\:\mathrm{an}\:\mathrm{example}, \\ $$$$\mathrm{lets}\:\mathrm{say}\:{S}\:\mathrm{contains}\:\mathrm{ten}\:\mathrm{random}\:\mathrm{integers}, \\ $$$$\mathrm{all}\:\mathrm{are}\:\mathrm{within}\:\mathrm{1}\leqslant{a}_{{k}} \leqslant\mathrm{10}. \\ $$$$\mathrm{What}\:\mathrm{would}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{average}\:\mathrm{be}? \\ $$
Commented by prakash jain last updated on 05/Dec/15
Same integer can be selected twice? or is the experiment with replacement?
$$\mathrm{Same}\:\mathrm{integer}\:\mathrm{can}\:\mathrm{be}\:\mathrm{selected}\:\mathrm{twice}?\:\mathrm{or}\:\mathrm{is} \\ $$$$\mathrm{the}\:\mathrm{experiment}\:\mathrm{with}\:\mathrm{replacement}? \\ $$
Commented by Filup last updated on 05/Dec/15
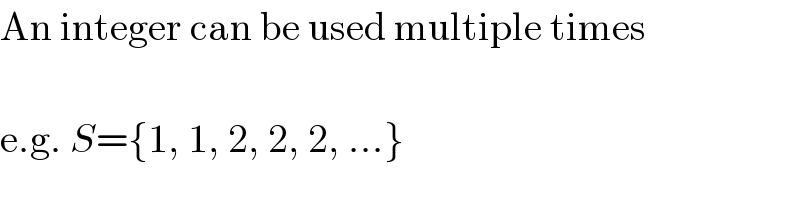
An integer can be used multiple times e.g. S={1, 1, 2, 2, 2, ...}
$$\mathrm{An}\:\mathrm{integer}\:\mathrm{can}\:\mathrm{be}\:\mathrm{used}\:\mathrm{multiple}\:\mathrm{times} \\ $$$$ \\ $$$$\mathrm{e}.\mathrm{g}.\:{S}=\left\{\mathrm{1},\:\mathrm{1},\:\mathrm{2},\:\mathrm{2},\:\mathrm{2},\:…\right\} \\ $$
Commented by Filup last updated on 05/Dec/15
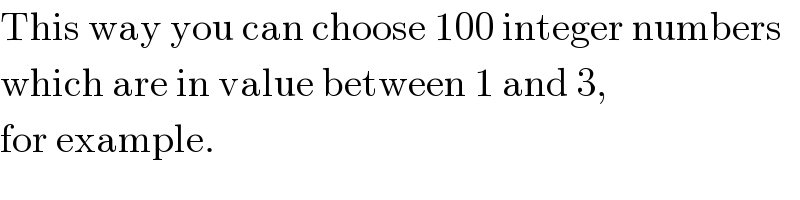
This way you can choose 100 integer numbers which are in value between 1 and 3, for example.
$$\mathrm{This}\:\mathrm{way}\:\mathrm{you}\:\mathrm{can}\:\mathrm{choose}\:\mathrm{100}\:\mathrm{integer}\:\mathrm{numbers} \\ $$$$\mathrm{which}\:\mathrm{are}\:\mathrm{in}\:\mathrm{value}\:\mathrm{between}\:\mathrm{1}\:\mathrm{and}\:\mathrm{3}, \\ $$$$\mathrm{for}\:\mathrm{example}. \\ $$
Commented by Filup last updated on 05/Dec/15
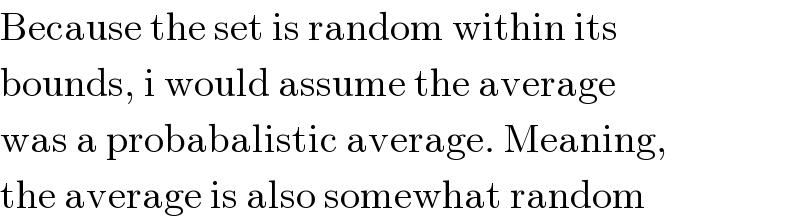
Because the set is random within its bounds, i would assume the average was a probabalistic average. Meaning, the average is also somewhat random
$$\mathrm{Because}\:\mathrm{the}\:\mathrm{set}\:\mathrm{is}\:\mathrm{random}\:\mathrm{within}\:\mathrm{its} \\ $$$$\mathrm{bounds},\:\mathrm{i}\:\mathrm{would}\:\mathrm{assume}\:\mathrm{the}\:\mathrm{average} \\ $$$$\mathrm{was}\:\mathrm{a}\:\mathrm{probabalistic}\:\mathrm{average}.\:\mathrm{Meaning}, \\ $$$$\mathrm{the}\:\mathrm{average}\:\mathrm{is}\:\mathrm{also}\:\mathrm{somewhat}\:\mathrm{random} \\ $$
Commented by Filup last updated on 05/Dec/15
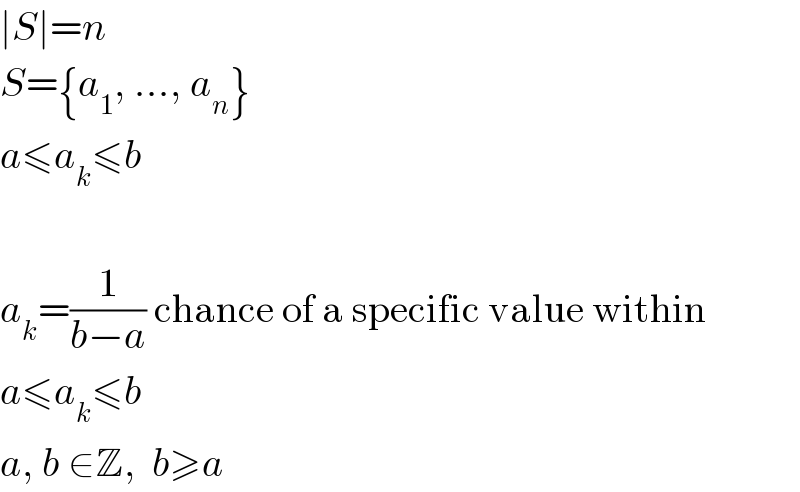
∣S∣=n S={a_1 , ..., a_n } a≤a_k ≤b a_k =(1/(b−a)) chance of a specific value within a≤a_k ≤b a, b ∈Z, b≥a
$$\mid{S}\mid={n} \\ $$$${S}=\left\{{a}_{\mathrm{1}} ,\:…,\:{a}_{{n}} \right\} \\ $$$${a}\leqslant{a}_{{k}} \leqslant{b} \\ $$$$ \\ $$$${a}_{{k}} =\frac{\mathrm{1}}{{b}−{a}}\:\mathrm{chance}\:\mathrm{of}\:\mathrm{a}\:\mathrm{specific}\:\mathrm{value}\:\mathrm{within} \\ $$$${a}\leqslant{a}_{{k}} \leqslant{b} \\ $$$${a},\:{b}\:\in\mathbb{Z},\:\:{b}\geqslant{a} \\ $$
Commented by prakash jain last updated on 05/Dec/15
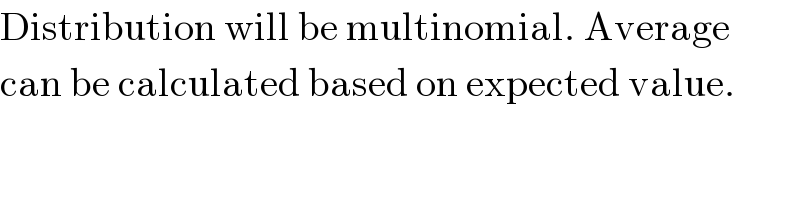
Distribution will be multinomial. Average can be calculated based on expected value.
$$\mathrm{Distribution}\:\mathrm{will}\:\mathrm{be}\:\mathrm{multinomial}.\:\mathrm{Average} \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{calculated}\:\mathrm{based}\:\mathrm{on}\:\mathrm{expected}\:\mathrm{value}. \\ $$
Answered by Filup last updated on 05/Dec/15
S={a_1 , ..., a_n }, a≤a_i ≤b, a_i ,a,b∈Z, b>a ∣S∣=n, n∈Z let a_n =b−k_n , 0≤k≤a, k_n ∈Z =random integer in range [a, b] for rnd k_n S^� =(1/n)Σ_(i=1) ^n a_i =((a_1 +...+a_n )/n) =(((b−k_1 )+(b−k_2 )+...+(b−k_n ))/n) =(1/n)Σ_(i=1) ^n (b−k_i ) =(1/n)bn−(1/n)Σ_(i=1) ^n k_i =b−(1/n)Σ_(i=1) ^n k_i S^� = b−(1/n)Σ_(i=1) ^n k_i where k_i =random integer 0≤k_i ≤a Note: this isnt a very good proof. it is practically the same as what is in the question. it is difficult to do maths with randomness
$${S}=\left\{{a}_{\mathrm{1}} ,\:…,\:{a}_{{n}} \right\},\:\:{a}\leqslant{a}_{{i}} \leqslant{b},\:\:{a}_{{i}} ,{a},{b}\in\mathbb{Z},\:\:\:{b}>{a} \\ $$$$\mid{S}\mid={n},\:\:{n}\in\mathbb{Z} \\ $$$$ \\ $$$$\mathrm{let}\:{a}_{{n}} ={b}−{k}_{{n}} ,\:\:\:\mathrm{0}\leqslant{k}\leqslant{a},\:{k}_{{n}} \in\mathbb{Z} \\ $$$$={random}\:\mathrm{integer}\:\mathrm{in}\:\mathrm{range}\:\left[{a},\:{b}\right]\:\mathrm{for}\:\mathrm{rnd}\:{k}_{{n}} \\ $$$$ \\ $$$$\bar {{S}}=\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} \\ $$$$=\frac{{a}_{\mathrm{1}} +…+{a}_{{n}} }{{n}} \\ $$$$=\frac{\left({b}−{k}_{\mathrm{1}} \right)+\left({b}−{k}_{\mathrm{2}} \right)+…+\left({b}−{k}_{{n}} \right)}{{n}} \\ $$$$=\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left({b}−{k}_{{i}} \right) \\ $$$$=\frac{\mathrm{1}}{{n}}{bn}−\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{k}_{{i}} \\ $$$$={b}−\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{k}_{{i}} \\ $$$$ \\ $$$$\bar {{S}}\:=\:{b}−\frac{\mathrm{1}}{{n}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{k}_{{i}} \\ $$$$\mathrm{where}\:{k}_{{i}} ={random}\:{integer}\:\:\mathrm{0}\leqslant{k}_{{i}} \leqslant{a} \\ $$$$ \\ $$$$\mathrm{Note}: \\ $$$$\mathrm{this}\:\mathrm{isnt}\:\mathrm{a}\:\mathrm{very}\:\mathrm{good}\:\mathrm{proof}.\:\mathrm{it}\:\mathrm{is}\:\mathrm{practically} \\ $$$$\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{what}\:\mathrm{is}\:\mathrm{in}\:\mathrm{the}\:\mathrm{question}. \\ $$$$\mathrm{it}\:\mathrm{is}\:\mathrm{difficult}\:\mathrm{to}\:\mathrm{do}\:\mathrm{maths}\:\mathrm{with}\:{randomness} \\ $$
Answered by prakash jain last updated on 05/Dec/15
Total number of integers=b−a+1 Probability of selecting any one value=(1/(b−a+1)) Expected number of times a given integer was selected after n trials=(n/(b−a+1)) Expectation is that a will be selcted (n/(b−a+1)) times. Same applies for a+1 to b. Expected sum =(n/(b−a+1))Σ_(i=a) ^b i Σ_(i=a) ^b i=((b−a+1)/2)(2a+(b−a+1−1)×1)=((b−a+1)/2)×(b+a) Expected Sum=(n/((b−a+1)))×(((b−a+1)(b+a))/2)=((n(b+a))/2) Expected average=(((n(b+a))/2)/n)=(((b+a))/2)
$$\mathrm{Total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{integers}={b}−{a}+\mathrm{1} \\ $$$$\mathrm{Probability}\:\mathrm{of}\:\mathrm{selecting}\:\mathrm{any}\:\mathrm{one}\:\mathrm{value}=\frac{\mathrm{1}}{{b}−{a}+\mathrm{1}} \\ $$$$\mathrm{Expected}\:\mathrm{number}\:\mathrm{of}\:\mathrm{times}\:\mathrm{a}\:\mathrm{given} \\ $$$$\mathrm{integer}\:\mathrm{was}\:\mathrm{selected}\:\mathrm{after}\:{n}\:\mathrm{trials}=\frac{{n}}{{b}−{a}+\mathrm{1}} \\ $$$$\mathrm{Expectation}\:\mathrm{is}\:\mathrm{that}\:{a}\:\mathrm{will}\:\mathrm{be}\:\mathrm{selcted}\:\frac{{n}}{{b}−{a}+\mathrm{1}}\:\mathrm{times}. \\ $$$$\mathrm{Same}\:\mathrm{applies}\:\mathrm{for}\:{a}+\mathrm{1}\:\mathrm{to}\:{b}. \\ $$$$\mathrm{Expected}\:\mathrm{sum}\:=\frac{{n}}{{b}−{a}+\mathrm{1}}\underset{{i}={a}} {\overset{{b}} {\sum}}{i} \\ $$$$\underset{{i}={a}} {\overset{{b}} {\sum}}{i}=\frac{{b}−{a}+\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}{a}+\left({b}−{a}+\mathrm{1}−\mathrm{1}\right)×\mathrm{1}\right)=\frac{{b}−{a}+\mathrm{1}}{\mathrm{2}}×\left({b}+{a}\right) \\ $$$$\mathrm{Expected}\:\mathrm{Sum}=\frac{{n}}{\left({b}−{a}+\mathrm{1}\right)}×\frac{\left({b}−{a}+\mathrm{1}\right)\left({b}+{a}\right)}{\mathrm{2}}=\frac{{n}\left({b}+{a}\right)}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Expected}\:\mathrm{average}=\frac{\frac{{n}\left({b}+{a}\right)}{\mathrm{2}}}{{n}}=\frac{\left({b}+{a}\right)}{\mathrm{2}} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *