Question Number 131305 by Algoritm last updated on 03/Feb/21

Answered by EDWIN88 last updated on 03/Feb/21
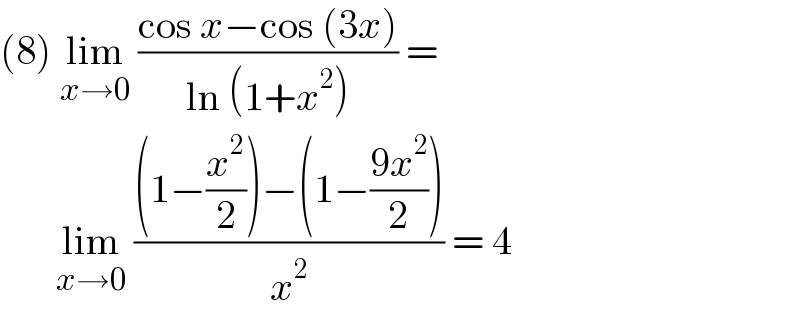
$$\left(\mathrm{8}\right)\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}−\mathrm{cos}\:\left(\mathrm{3}{x}\right)}{\mathrm{ln}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:=\: \\ $$$$\:\:\:\:\:\:\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)−\left(\mathrm{1}−\frac{\mathrm{9}{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{{x}^{\mathrm{2}} }\:=\:\mathrm{4}\: \\ $$
Answered by EDWIN88 last updated on 03/Feb/21
![(6) f ′(1) = lim_(x→0) ((f(1+x)−f(1))/x) f ′(1)= lim_(x→0) (((√(x+4))−(√4))/x) f ′(1) = lim_(x→0) [ (x/(x [(√(x+4)) +(√4) ])) ] = (1/4)](https://www.tinkutara.com/question/Q131308.png)
$$\:\left(\mathrm{6}\right)\:{f}\:'\left(\mathrm{1}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left(\mathrm{1}+{x}\right)−{f}\left(\mathrm{1}\right)}{{x}} \\ $$$$\:\:\:\:\:{f}\:'\left(\mathrm{1}\right)=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{{x}+\mathrm{4}}−\sqrt{\mathrm{4}}}{{x}} \\ $$$$\:\:\:{f}\:'\left(\mathrm{1}\right)\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\:\frac{{x}}{{x}\:\left[\sqrt{{x}+\mathrm{4}}\:+\sqrt{\mathrm{4}}\:\right]}\:\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\: \\ $$
Answered by EDWIN88 last updated on 03/Feb/21
![(10) ∫_0 ^( 4) ((x^3 dx)/( (√(x^2 +2)))) let x^2 +2 = p^2 ⇒x dx = p dp → determinant (((x=4→p=3(√2))),((x=0→p=(√2)))) E = ∫_(√2) ^( 3(√2)) (((p^2 −2) p dp)/p) E= [(1/3)p^3 −2p ]_(√2) ^(3(√2)) = ((1/3)p [ p^2 −6 ])_(√2) ^(3(√2)) E= (1/3){ 3(√2) . 12−(√2) .(−4) } E = (1/3).40(√2) = ((40(√2))/3)](https://www.tinkutara.com/question/Q131310.png)
$$\left(\mathrm{10}\right)\:\int_{\mathrm{0}} ^{\:\mathrm{4}} \:\frac{{x}^{\mathrm{3}} \:{dx}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{2}}}\: \\ $$$$\:{let}\:{x}^{\mathrm{2}} +\mathrm{2}\:=\:{p}^{\mathrm{2}} \:\Rightarrow{x}\:{dx}\:=\:{p}\:{dp}\:\rightarrow\begin{array}{|c|c|}{{x}=\mathrm{4}\rightarrow{p}=\mathrm{3}\sqrt{\mathrm{2}}}\\{{x}=\mathrm{0}\rightarrow{p}=\sqrt{\mathrm{2}}}\\\hline\end{array} \\ $$$${E}\:=\:\int_{\sqrt{\mathrm{2}}} ^{\:\mathrm{3}\sqrt{\mathrm{2}}} \frac{\left({p}^{\mathrm{2}} −\mathrm{2}\right)\:{p}\:{dp}}{{p}} \\ $$$${E}=\:\left[\frac{\mathrm{1}}{\mathrm{3}}{p}^{\mathrm{3}} −\mathrm{2}{p}\:\right]_{\sqrt{\mathrm{2}}} ^{\mathrm{3}\sqrt{\mathrm{2}}} =\:\left(\frac{\mathrm{1}}{\mathrm{3}}{p}\:\left[\:{p}^{\mathrm{2}} −\mathrm{6}\:\right]\right)_{\sqrt{\mathrm{2}}} ^{\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$${E}=\:\frac{\mathrm{1}}{\mathrm{3}}\left\{\:\mathrm{3}\sqrt{\mathrm{2}}\:.\:\mathrm{12}−\sqrt{\mathrm{2}}\:.\left(−\mathrm{4}\right)\:\right\} \\ $$$${E}\:=\:\frac{\mathrm{1}}{\mathrm{3}}.\mathrm{40}\sqrt{\mathrm{2}}\:=\:\frac{\mathrm{40}\sqrt{\mathrm{2}}}{\mathrm{3}} \\ $$
Answered by Ar Brandon last updated on 03/Feb/21
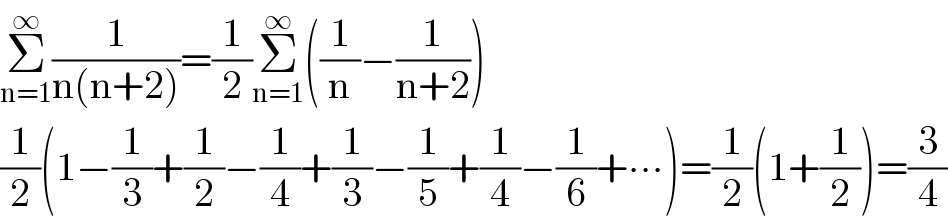
$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{2}}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{6}}+\centerdot\centerdot\centerdot\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{3}}{\mathrm{4}} \\ $$
