Question Number 133692 by Dwaipayan Shikari last updated on 23/Feb/21

$$\frac{{sin}\mathrm{1}}{{e}}−\frac{{sin}\left(\mathrm{2}\right)}{\mathrm{2}{e}^{\mathrm{2}} }+\frac{{sin}\left(\mathrm{3}\right)}{\mathrm{3}{e}^{\mathrm{3}} }−\frac{{sin}\left(\mathrm{4}\right)}{\mathrm{4}{e}^{\mathrm{4}} }+…={tan}^{−\mathrm{1}} \left(\frac{{sin}\left(\mathrm{1}\right)}{{cos}\left(\mathrm{1}\right)+{e}}\right) \\ $$
Commented by Dwaipayan Shikari last updated on 23/Feb/21

$${Share}\:{an}\:{Idea}\:{to}\:{solve}\:{this}.{I}\:{have}\:{a}\:{strange}\:{way}\:{but}\:{i}\:{want}\: \\ $$$${to}\:{see}\:{other}'{s}\:{perspective}\:? \\ $$
Answered by mindispower last updated on 23/Feb/21

$$=\frac{{sin}\left({k}\right)}{{ne}^{{k}} }={Im}\underset{{m}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{m}} \frac{{e}^{{im}} }{{me}^{{m}} } \\ $$$$={Im}−{ln}\left(\mathrm{1}+{e}^{\left({i}−\mathrm{1}\right)} \right) \\ $$$$=−\:{arg}\left(\mathrm{1}+{e}^{{i}} .{e}^{−\mathrm{1}} \right)=−{tg}^{−} \left(\frac{{e}^{−\mathrm{1}} {sin}\left(\mathrm{1}\right)}{\mathrm{1}+{e}^{−\mathrm{1}} {cos}\left(\mathrm{1}\right)}\right) \\ $$$$=−{tg}^{−} \left(\frac{{sin}\left(\mathrm{1}\right)}{{e}+{cos}\left(\mathrm{1}\right)}\right)=\frac{\pi}{\mathrm{2}}−{tg}^{−} \left(\frac{{e}+{cos}\left(\mathrm{1}\right)}{{sin}\left(\mathrm{1}\right)}\right) \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 23/Feb/21

$${Sir}\:{first}\:{line}\:\underset{{m}\geqslant\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{m}+\mathrm{1}} }{{me}}{e}^{{im}} \\ $$
Commented by mindispower last updated on 23/Feb/21

$${thanx}\:{yes}\:{sir}\:{sorry}\:{too}\:{busy}\:{this}\:{days}\: \\ $$$${back}\:{soon} \\ $$
Answered by Dwaipayan Shikari last updated on 23/Feb/21
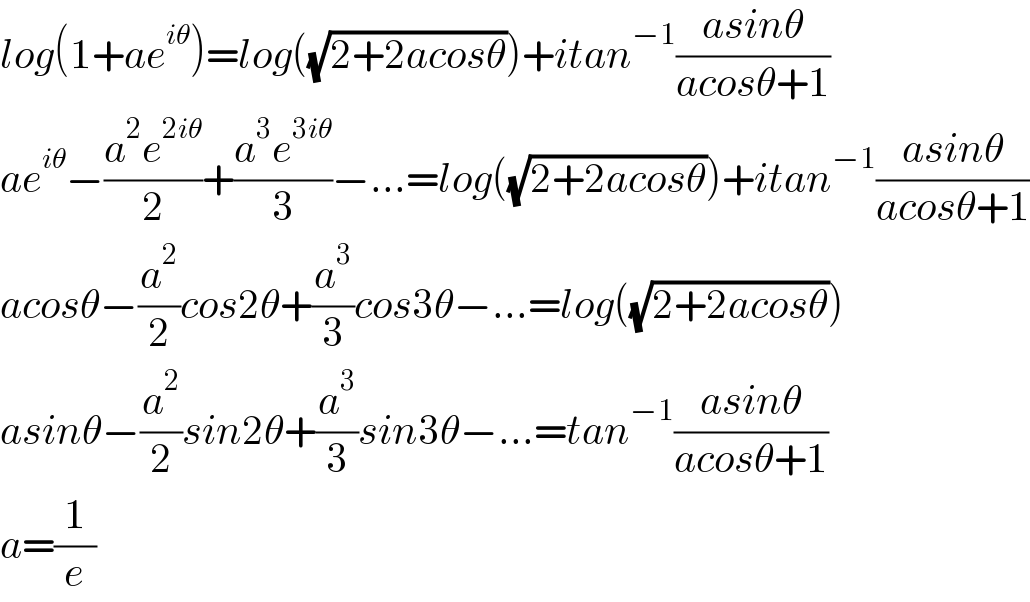
$${log}\left(\mathrm{1}+{ae}^{{i}\theta} \right)={log}\left(\sqrt{\mathrm{2}+\mathrm{2}{acos}\theta}\right)+{itan}^{−\mathrm{1}} \frac{{asin}\theta}{{acos}\theta+\mathrm{1}} \\ $$$${ae}^{{i}\theta} −\frac{{a}^{\mathrm{2}} {e}^{\mathrm{2}{i}\theta} }{\mathrm{2}}+\frac{{a}^{\mathrm{3}} {e}^{\mathrm{3}{i}\theta} }{\mathrm{3}}−…={log}\left(\sqrt{\mathrm{2}+\mathrm{2}{acos}\theta}\right)+{itan}^{−\mathrm{1}} \frac{{asin}\theta}{{acos}\theta+\mathrm{1}} \\ $$$${acos}\theta−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{cos}\mathrm{2}\theta+\frac{{a}^{\mathrm{3}} }{\mathrm{3}}{cos}\mathrm{3}\theta−…={log}\left(\sqrt{\mathrm{2}+\mathrm{2}{acos}\theta}\right) \\ $$$${asin}\theta−\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{sin}\mathrm{2}\theta+\frac{{a}^{\mathrm{3}} }{\mathrm{3}}{sin}\mathrm{3}\theta−…={tan}^{−\mathrm{1}} \frac{{asin}\theta}{{acos}\theta+\mathrm{1}} \\ $$$${a}=\frac{\mathrm{1}}{{e}} \\ $$
