Question Number 65992 by naka3546 last updated on 07/Aug/19
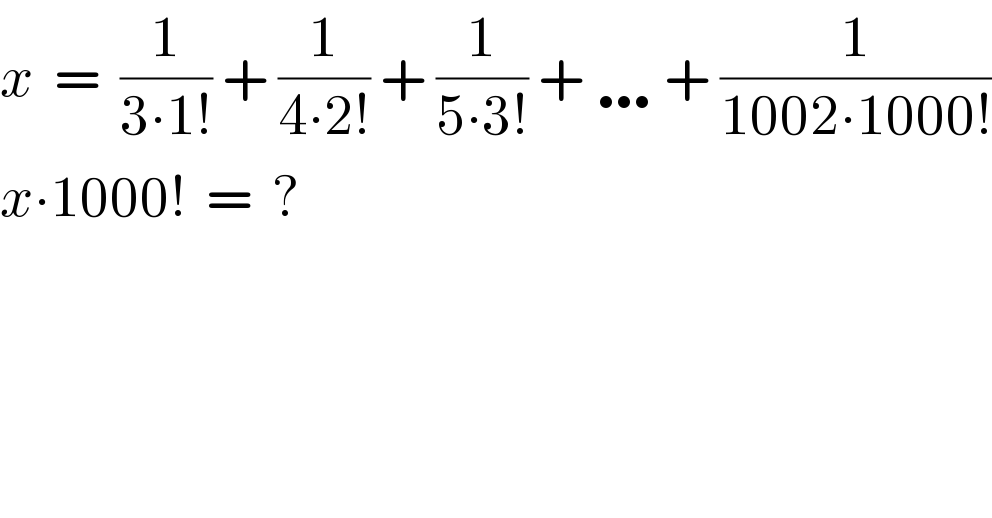
$${x}\:\:=\:\:\frac{\mathrm{1}}{\mathrm{3}\centerdot\mathrm{1}!}\:+\:\frac{\mathrm{1}}{\mathrm{4}\centerdot\mathrm{2}!}\:+\:\frac{\mathrm{1}}{\mathrm{5}\centerdot\mathrm{3}!}\:+\:\ldots\:+\:\frac{\mathrm{1}}{\mathrm{1002}\centerdot\mathrm{1000}!} \\ $$$${x}\centerdot\mathrm{1000}!\:\:=\:\:? \\ $$
Commented by Prithwish sen last updated on 08/Aug/19
![last term (n/((n+1)!)) where n= 1001 ∴ [((n+1−1)/((n+1)!))] = (1/(n!)) − (1/((n+1)!)) ∴ x = (2/(3!))+(3/(4!))+...+((1001)/(1002! )) = (1/(2!))−(1/(3!))+(1/(3!))−(1/(4!))+...+(1/(1001!)) −(1/(1002!)) =(1/(2!))−(1/(1002!))](https://www.tinkutara.com/question/Q66049.png)
$$\mathrm{last}\:\mathrm{term}\:\frac{\mathrm{n}}{\left(\mathrm{n}+\mathrm{1}\right)!}\:\:\mathrm{where}\:\mathrm{n}=\:\mathrm{1001} \\ $$$$\therefore\:\left[\frac{\mathrm{n}+\mathrm{1}−\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!}\right]\:=\:\frac{\mathrm{1}}{\mathrm{n}!}\:−\:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)!} \\ $$$$\therefore\:\mathrm{x}\:=\:\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{3}}{\mathrm{4}!}+…+\frac{\mathrm{1001}}{\mathrm{1002}!\:}\:=\:\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}+…+\frac{\mathrm{1}}{\mathrm{1001}!}\:−\frac{\mathrm{1}}{\mathrm{1002}!} \\ $$$$\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{1002}!} \\ $$
Answered by $@ty@m123 last updated on 07/Aug/19

$${x}=\frac{\mathrm{2}}{\mathrm{3}!}+\frac{\mathrm{3}}{\mathrm{4}!}+….+\frac{\mathrm{1001}}{\mathrm{1002}!} \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{4}}{\mathrm{4}!}−\frac{\mathrm{1}}{\mathrm{4}!}+….+\frac{\mathrm{1002}}{\mathrm{1002}!}−\frac{\mathrm{1}}{\mathrm{1002}!} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}+\frac{\mathrm{1}}{\mathrm{3}!}−\frac{\mathrm{1}}{\mathrm{4}!}+……+\frac{\mathrm{1}}{\mathrm{1001}!}−\frac{\mathrm{1}}{\mathrm{1002}!} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{1002}!} \\ $$$${x}.\mathrm{1000}!=\frac{\mathrm{1000}!}{\mathrm{2}}−\frac{\mathrm{1000}!}{\mathrm{1002}!} \\ $$$${x}.\mathrm{1000}!=\frac{\mathrm{1000}!}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{1002}.\mathrm{1001}} \\ $$$${x}.\mathrm{1000}!=\frac{\mathrm{501}.\mathrm{1001}!−\mathrm{1}}{\mathrm{1002}.\mathrm{1001}} \\ $$$$ \\ $$
Commented by Prithwish sen last updated on 07/Aug/19

$$\mathrm{beautiful}. \\ $$
